【题目】水果市场中的甲、乙两家商店中都批发同一种水果,批发水果x千克时,在甲、乙两家商店的批发价分别为y1元和y2元,已知y1和y2关于x的函数图象分别为如图所示的折线OAB和射线OC. 
(1)请求出y2与自变量x的函数解析式,并写出自变量x的取值范围;
(2)当乙商店的批发价比甲商店的批发价便宜时,根据函数图象直接写出自变量x的取值范围;
(3)如果批发30千克水果时,在甲店批发比在乙店批发便宜50元,求射线AB的函数解析式并写出自变量x的取值范围.
参考答案:
【答案】
(1)解:∵射线OC经过原点,
∴设y2与自变量x的函数关系为y2=k'x(k'≠0),
∵射线OC经过点(20,200),
∴200=20k',
解得k'=10.
∴y2=10x,自变量x的取值范围是x>0
(2)解:由图象可知,当0<x<20时,在乙店批发比较便宜.
(3)解:∵射线OC过点(20,200),射线OC的表达式是y2=10x,
过点(30,0)作y轴的平行线,交OC于点E,交AB于点F.
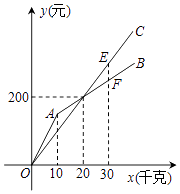
∴E(30,300),F(30,250),
设射线AB的表达式为y1=kx+b,
∴ ![]() ,解得
,解得 ![]() .
.
∴射线AB的表达式为y1=5x+100,自变量x的取值范围是x>10.
【解析】(1)根据射线OC经过点(20,200),即可得到y2与自变量x的函数解析式以及自变量x的取值范围;(2)由图象可知,当0<x<20时,在乙店批发比较便宜;(3)过点(30,0)作y轴的平行线,交OC于点E,交AB于点F,即可得到E(30,300),F(30,250),再根据待定系数法进行计算,即可得到射线AB的函数解析式以及自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值小于4的所有整数的和是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式2xy-x2-y2分解因式的结果是( )
A. (x+y)2 B. -(x+y)2 C. (x-y)2 D. -(x-y)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.

(1)求时间t的取值范围;
(2)当四边形ABQP为矩形时,求时间t的值;
(3)是否存在时间t的值,使得△APQ的面积是△ABC的面积的一半?若存在,请求出t的值,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x+k的图象大致是( )
A.
B.
C.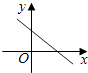
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校就“遇见路人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查,图1和图2是整理数据后绘制的两幅不完整的统计图. 请根据图中提供的信息,解答下列问题:
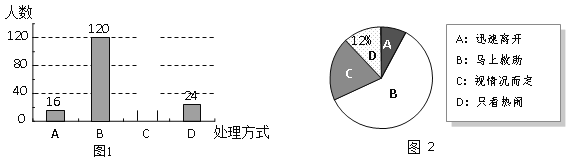
(1)该校随机抽查了 名学生?请将图1补充完整;
(2)在图2中,“视情况而定”部分所占的圆心角是 度;
(3)在这次调查中,甲、乙、丙、丁四名学生都选择“马上救助”,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为5,P为⊙O上一点,P(4,3),PC、PD为⊙O的弦,分别交y轴正半轴于E、F,且PE=PF,连CD,设直线CD为y=kx+b,则k=______.

相关试题

