【题目】一次函数![]() 与一次函数
与一次函数![]() 的图象的交点的纵坐标为
的图象的交点的纵坐标为![]() ,
, ![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 时,求证:
时,求证:![]() .
.
参考答案:
【答案】(1)1;(2)证明见解析.
【解析】
(1)联立一次函数解析式,根据交点纵坐标为![]() ,可一求得交点横坐标为1,进而得到a +b +c =2,对所给式子
,可一求得交点横坐标为1,进而得到a +b +c =2,对所给式子![]() 进行化简,将a +b +c =2代入即可求出
进行化简,将a +b +c =2代入即可求出![]() 的值;
的值;
(2)a + b + c =2,平方化简得a2 + b2 + c2 = 4-2×1 = 2,对所求证的式子进行变形得,(b-a)[1-2(a + b) + (b2 + a2 + ab)] = 0,分类进行讨论即可.
(1)依题意得:![]() ,且abc≠0,
,且abc≠0,
由①得:x=1,代入②得:a + b + c =2
![]()
a3 + b3 + c3-3abc-2(a2 + b2 + c2) + (a + b + c) = 0
(a + b + c)(a2 + b2 + c2-ab-bc-ca)-2(a2 + b2 + c2) + (a + b + c) = 0
2(a2 + b2 + c2-ab-bc-ca)-2(a2 + b2 + c2) + 2 = 0
ab + bc + ca = 1
(2)(a + b + c)2 = 22 = a2 + b2 + c2 + 2(ab + bc + ca)
a2 + b2 + c2 = 4-2×1 = 2
当![]() 时,要证:
时,要证:![]() ,
,
只需证:b(1-b)2 = a(1-a)2
b(1-b)2-a(1-a)2 = 0
b-a-2(b2-a2) + (b3-a3) = 0
(b-a)[1-2(a + b) + (b2 + a2 + ab)] = 0 (*)
i)当a = b时,(*)式显然成立;
ii)当a≠b时,
∵ a + b + c = 2,a2 + b2 + c2 = 2,ab + bc + ca = 1
∴ a + b = 2-c,a2 + b2 = 2-c2,ab = 1-c(a + b) = 1-c(2-c)
∴ 1-2(a + b) + (b2 + a2 + ab) = 1-2(2-c) + 2-c2 + 1-c(2-c)
= 1-4+2c+2-c2+1-2c+c2
= 0
∴ (*)式成立.
综上,当![]() 时,均有
时,均有![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠A = 3∠C = 90,AB = 3,点Q在边AB上且BQ =
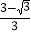 ,过Q作QF∥BC交AC于点F,点P在线段QF上,过P作PD∥AC交AB于点D,PE∥AB交BC于点E,当P到△ABC的三边的距离之和为3时,PD + PE + PF =_________.
,过Q作QF∥BC交AC于点F,点P在线段QF上,过P作PD∥AC交AB于点D,PE∥AB交BC于点E,当P到△ABC的三边的距离之和为3时,PD + PE + PF =_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】算式:1△1△1=□,在每一个“△”中添加运算符号“+”或“﹣”后,通过计算,“□”中可得到不同的运算结果.求运算结果为1的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,AB=CD,点E、F在BC上,且BE=CF.
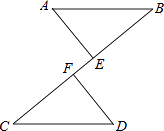
(1)求证:△ABE≌△DCF;
(2)试证明:以A、F、D、E为顶点的四边形是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市对一大型超市销售的甲、乙、丙3种大米进行质量检测.共抽查大米200袋,质量评定分为A、B两个等级(A级优于B级),相应数据的统计图如下:
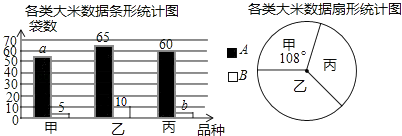
根据所给信息,解决下列问题:
(1)a= , b=;
(2)已知该超市现有乙种大米750袋,根据检测结果,请你估计该超市乙种大米中有多少袋B级大米?
(3)对于该超市的甲种和丙种大米,你会选择购买哪一种?运用统计知识简述理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明在教学楼上的窗口A看地面上的B、C两个花坛,测得俯角∠EAB=30°,俯角∠EAC=45°.已知教学楼基点D与点C、B在同一条直线上,且B、C两花坛之间的距离为6m.求窗口A到地面的高度AD.(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的函数图像与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30.
的函数图像与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,
 ),试用含m的代数式表示四边形AOPB的面积,并求当△APB与△ABC面积相等时m的值;
),试用含m的代数式表示四边形AOPB的面积,并求当△APB与△ABC面积相等时m的值;(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出Q的所有可能的坐标;若不存在,请说明理由.
相关试题

