【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?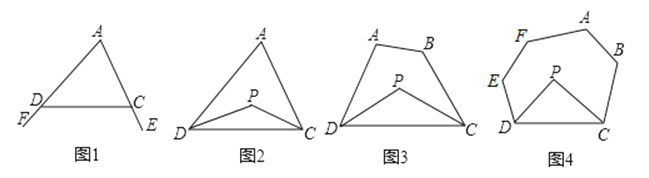
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系
参考答案:
【答案】解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;
探究二:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD,
∠ACD,
=180°﹣![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°﹣![]() (180°﹣∠A),
(180°﹣∠A),
=90°+![]() ∠A;
∠A;
探究三:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠BCD,
∠BCD,
=180°﹣![]() (∠ADC+∠BCD),
(∠ADC+∠BCD),
=180°﹣![]() (360°﹣∠A﹣∠B),
(360°﹣∠A﹣∠B),
=![]() (∠A+∠B);
(∠A+∠B);
探究四:六边形ABCDEF的内角和为:(6﹣2)180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠P=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠P=180°﹣∠PDC﹣∠PCD,
=180°﹣![]() ∠ADC﹣
∠ADC﹣![]() ∠ACD,
∠ACD,
=180°﹣![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°﹣![]() (720°﹣∠A﹣∠B﹣∠E﹣∠F),
(720°﹣∠A﹣∠B﹣∠E﹣∠F),
=![]() (∠A+∠B+∠E+∠F)﹣180°,
(∠A+∠B+∠E+∠F)﹣180°,
即∠P=![]() (∠A+∠B+∠E+∠F)﹣180°.
(∠A+∠B+∠E+∠F)﹣180°.
【解析】探究一:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根据三角形内角和定理整理即可得解;
探究二:根据角平分线的定义可得∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,然后根据三角形内角和定理列式整理即可得解;
∠ACD,然后根据三角形内角和定理列式整理即可得解;
探究三:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;
探究四:根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可
-
科目: 来源: 题型:
查看答案和解析>>【题目】运用等式的性质进行变形时,下列各式中,不一定正确的是( )
A. 如果a=b,那么a-c=b-c B. 如果a=b,那么a+c=b+c
C. 如果a=b,那么ab=ac D. 如果a=b,那么ac=bc
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:﹣|﹣3|=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC+∠ECB=180°,∠P=∠Q,
(1)AB与ED平行吗?为什么?
(2)∠1与∠2是否相等?说说你的理由.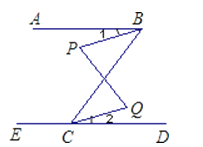
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某工艺品厂生产一款工艺品,已知这款工艺品的生产成本为每件60元,经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系.
售价x(元)
…
70
90
…
销售量y(件)
…
3000
1000
…
(1)求销售量y(件)与售价x(元)之间的函数表达式.
(2)当售价为80元时,工艺品厂每天获得的利润为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为了保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
(3)当每斤的售价定为多少元时,每天获利最大?最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式,并写出y<0时,对应x的取值范围;
(2)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.
①当BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a,b),将矩形ABCD的周长L表示为a的函数并写出自变量的取值范围,判断周长是否存在最大值?如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
相关试题

