【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式,并写出y<0时,对应x的取值范围;
(2)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.
①当BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a,b),将矩形ABCD的周长L表示为a的函数并写出自变量的取值范围,判断周长是否存在最大值?如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
参考答案:
【答案】(1)y<0时,0<x<3;(2)①矩形的周长为6;②当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)根据待定系数法,可得函数解析式,根据函数的增减性,可得符合条件的函数解析式,根据函数与不等式的关系,可得答案;
(2)①根据BC关于对称轴对称,可得A点的纵坐标,根据矩形的周长公式,可得答案;
②分类讨论A在对称轴左侧,A在对称轴右侧,根据对称,可得BC的长,AB的长,根据周长公式,可得函数解析式,根据函数的增减性,可得答案.
试题解析:(1)∵抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点(0,0),∴m2﹣1=0,∴m=±1,
∴y=x2+x或y=x2﹣3x,∵当x<0时,y随x的增大而减小,∴y=x2﹣3x,由函数与不等式的关系,得y<0时,0<x<3;
(2)①如图1
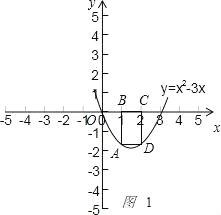 ,
,
当BC=1时,由抛物线的对称性,得点A的纵坐标为﹣2,
∴矩形的周长为6;
②∵A的坐标为(a,b),
∴当点A在对称轴左侧时,如图2
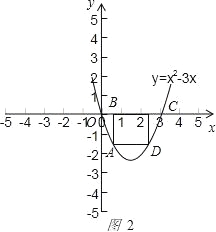 ,
,
矩形ABCD的一边BC=3﹣2a,另一边AB=3a﹣a2,
周长L=﹣2a2+2a+6.其中0<a<![]() ,当a=
,当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() ),
),
当点A在对称轴右侧时如图3
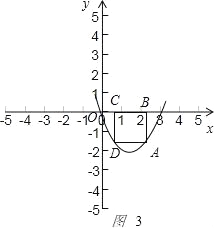 ,
,
矩形的一边BC=3﹣(6﹣2a)=2a﹣3,另一边AB=3a﹣a2,
周长L=﹣2a2+10a﹣6,其中![]() <a<3,当a=
<a<3,当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() );
);
综上所述:当0<a<![]() 时,L=﹣2(a﹣
时,L=﹣2(a﹣![]() )2+
)2+![]() ,
,
∴当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() ),
),
当![]() <a<3时,L=﹣2(a﹣
<a<3时,L=﹣2(a﹣![]() )2+
)2+![]() ,
,
∴当a=![]() 时,L最大=
时,L最大=![]() ,A点坐标为(
,A点坐标为(![]() ,﹣
,﹣![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列表述,能确定具体位置的是( )
A. 某电影院2排 B. 大桥南路 C. 北偏东30° D. 东经108°,北纬43°
-
科目: 来源: 题型:
查看答案和解析>>【题目】34°25′20″×3+35°42′.
-
科目: 来源: 题型:
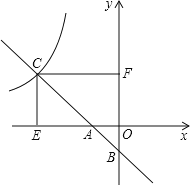
查看答案和解析>>【题目】如图,一次函数y1=mx+n的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=
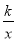 (x<0)交于点C,过点C分别作x轴、y轴的垂线,垂足分别为点E、F.若OB=2,CF=6,
(x<0)交于点C,过点C分别作x轴、y轴的垂线,垂足分别为点E、F.若OB=2,CF=6,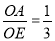 .
.
(1)求点A的坐标;
(2)求一次函数和反比例函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如下表所示:
国外品牌
国内品牌
进价(元/部)
4400
2000
售价(元/部)
5000
2500
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可毛获利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张大伯共有7块麦田,今年的收成与去年相比(增产为正,减产为负)情况如下(单位:kg):+320,-170,-320,+130,+150,+40,-150.则今年小麦的总产量与去年相比( )
A. 增产20 kg B. 减产20 kg C. 增长120 kg D. 持平
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件属于必然事件的是( )
A. 蒙上眼睛射击正中靶心
B. 买一张彩票一定中奖
C. 打开电视机,电视正在播放新闻联播
D. 月球绕着地球转
相关试题

