【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).

参考答案:
【答案】1900米
【解析】试题分析:设EC=x,则在RT△BCE中,用x表示出BE的长,在Rt△ACE中,再用x表示出AE的长,根据AB+BE=AE,列出方程,解方程即可得出答案.
试题解析:设EC=x,
在Rt△BCE中,tan∠EBC=![]() ,
,
则BE= ![]() ,
,
在Rt△ACE中,tan∠EAC=![]() ,
,
则AE= ![]() ,
,
∵AB+BE=AE,
∴300+ ![]() =x,
=x,
解得:x=1800,
即可得山高CD=DE-EC=3700-1800=1900(米).
答:这座山的高度是1900米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每天薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的( )
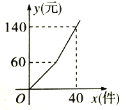
A.a=20
B.b=4
C.若工人甲一天获得薪金180元,则他共生产45件.
D.人乙一天生产40(件),则他获得薪金140元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=115°,∠ACF=25°,则∠FEC=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一长方形鸡场,鸡场的一边靠墙(墙长 18 米),另三边用竹篱笆围成,竹篱笆的总长为 35 米,与墙平行的边留有 1 米宽的门(门用其它材料做成),若鸡场的面积为 160 平方米,则鸡场与墙垂直的边长为( )

A.7.5 米B.8米C.10米D.10米或8米
-
科目: 来源: 题型:
查看答案和解析>>【题目】画出函数y1=-x+1,y2=2x-5 的图象,利用图象回答下列问题:

(1)方程组
 的解是_______________.
的解是_______________.(2)y1随x增大而_________, y2随x增大而________.
(3)当y1>y2时,x的取值范围 是_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:直线AB∥CD,点M,N分别在直线AB,CD上,点E为平面内一点.
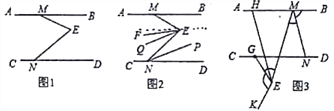
(1)如图1,∠BME,∠E,∠END的数量关系为 (直接写出答案);
(2)如图2,∠BME=m°,EF平分∠MEN,NP平分∠END,EQ∥NP,求∠FEQ的度数(用用含m的式子表示)
(3)如图3,点G为CD上一点,∠BMN=n·∠EMN,∠GEK=n·∠GEM,EH∥MN交AB于点H,探究∠GEK,∠BMN,∠GEH之间的数量关系(用含n的式子表示)
相关试题

