【题目】如图,在ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.

(1)作△ACD外接圆⊙O(尺规作图,保留作图痕迹,不写作法);
(2)判断直线BC与⊙O的位置关系,并证明你的结论.
参考答案:
【答案】(1)见解析;(2)BC与⊙O相切.
【解析】
试题分析:(1)先作线段AD的垂直平分线交AD于O点,然后以O为圆心,OA为半径画圆即可;
(2)连接CO,如图,利用三角形外角性质得到∠COB=2∠A=60°,则∠COB+∠B=90°,所以∠OCB=90°,然后根据切线的判定定理可判断BC与⊙O相切.
解:(1)如图,⊙O为所作;
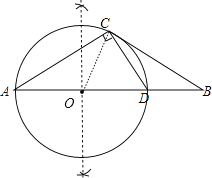
(2)BC与⊙O相切.
证明如下:连接CO,如图,
∵∠A=∠B=30°,
∴∠COB=2∠A=60°,
∴∠COB+∠B=30°+60°=90°,
∴∠OCB=90°,
∴OC⊥BC,
又BC经过半径OC的外端点C,
∴BC与⊙O相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=-(k-1)x+5随着x的增大,y的值也增大,那么k的取值范围是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:2a﹣7和a+4是某正数的平方根,b﹣7的立方根为﹣2.
(1)求:a、b的值;
(2)求a+b的算术平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=﹣
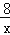 的图象与线段AB交于M点,且AM=BM,过点M作MC⊥x轴于点C,MD⊥y轴于点D.
的图象与线段AB交于M点,且AM=BM,过点M作MC⊥x轴于点C,MD⊥y轴于点D.
(1)求证:MC=MD;
(2)求点M的坐标;
(3)求直线AB的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:
①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
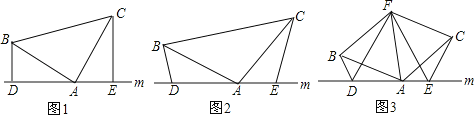
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.猜测DE、BD、CE三条线段之间的数量关系(直接写出结果即可).
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问第(1)题中DE、BD、CE之间的关系是否仍然成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断线段DF、EF的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
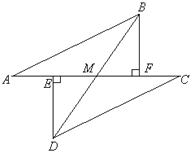
(1)试猜想DE与BF的关系,并证明你的结论;
(2)求证:MB=MD.
相关试题

