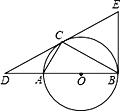
【题目】已知△ABC内接于以AB为直径的⊙O，过点C作⊙O的切线交BA的延长线于点D，且DA∶AB=1∶2．
（1）求∠CDB的度数；
（2）在切线DC上截取CE=CD，连接EB，判断直线EB与⊙O的位置关系，并证明．
【答案】（1）
；（2）直线EB与
相切，证明见解析.
【解析】试题分析：（1）根据DA:AB=1:2，得到DA等于圆的半径．连接过切点的半径，构造直角三角形，利用解直角三角形的知识求解；
（2）连接OC．根据（1）中的结论，可以知道直角
有一个角为30°．根据圆周角定理发现
得到
进一步得到等边
．则
根据切线的判定即可证明．
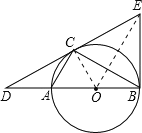
试题解析：(1)如图，连接OC，
∵CD是的切线，
设的半径为R，则AB=2R，
∵DA:AB=1:2，
∴DA=R，DO=2R.
在Rt△DOC中, 
即
(2)直线EB与相切，
证明：连接OC，
由(1)可知
∵OC=OB，
∴∠CBD=∠CDB.
∴CD=CB.
∵CD是的切线，
又∵CD=CE，
∴CB=CE.
∴△CBE为等边三角形,
∴EB是的切线.
科目：初中数学 来源： 题型：
【题目】已知抛物线l1与l2形状相同，开口方向不同，其中抛物线l1：y=ax2﹣8ax﹣
交x轴于A，B两点（点A在点B的左侧），且AB=6；抛物线l2与l1交于点A和点C（5，n）．
（1）求抛物线l1，l2的表达式；
（2）当x的取值范围是 时，抛物线l1与l2上的点的纵坐标同时随横坐标的增大而增大；
（3）直线MN∥y轴，交x轴，l1，l2分别相交于点P（m，0），M，N，当1≤m≤7时，求线段MN的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：直线MN，PQ被射线BA截于A，B两点，且MN∥PQ，点D是直线MN上一定点，C是射线BA上一动点，连结CD，过点C作CE⊥CD交直线PQ于点E．
（1）若点C在线段AB上．
①依题意，补全图形；
②请写出∠ADC和∠CEB的数量关系，并证明．
（2）若点C在线段BA的延长线上，直接写出∠ADC和∠CEB的数量关系，不必证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示，现将△ABC平移，使点A变换为点A'，点B'、C'分别是B、C的对应点．
（1）请画出平移后的△A'B'C'；
（2）若连接AA'，CC'，则这两条线段之间的关系是 ．
（3）作直线MN，将△ABC分成两个面积相等的三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于一元二次方程ax2+bx+c=0 （a≠0），下列说法中错误的是（ ）
A. 当a＞0，c＜0时，方程一定有实数根
B. 当c=0时，方程至少有一个根为0
C. 当a＞0，b=0，c＜0时，方程的两根一定互为相反数
D. 当abc＜0时，方程的两个根同号，当abc＞0时，方程的两个根异号
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图（1），△ABC和△EDC中，D为△ABC边AC上一点，CA平分∠BCE，BC＝CD，AC＝CE．
（1）求证：∠A＝∠CED；
（2）如图（2），若∠ACB＝60°，连接BE交AC于F，G为边CE上一点，满足CG＝CF，连接DG交BE于H．
①求∠DHF的度数；
②若EB平分∠DEC，试说明：BE平分∠ABC．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知：∠MON=30°，点A1、A2、A3、…在射线ON上，点B1、B2、B3、…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形，若OA1=1，则△A9B9A10的边长为（ ）
A. 32 B. 64 C. 128 D. 256
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
