【题目】若多项式x2+ax+b可分解为(x+1)(x﹣2),试求a,b的值.
参考答案:
【答案】解:由题意,得x2+ax+b=(x+1)(x﹣2).
而(x+1)(x﹣2)=x2﹣x﹣2,
所以x2+ax+b=x2﹣x﹣2.
比较两边系数,得a=﹣1,b=﹣2.
【解析】计算(x+1)(x﹣2)的结果中,x的一次项系数为a,常数项为b.
【考点精析】根据题目的已知条件,利用因式分解的定义的相关知识可以得到问题的答案,需要掌握因式分解的最后结果必须是几个整式的乘积,否则不是因式分解;因式分解的结果必须进行到每个因式在有理数范围内不能再分解为止.
-
科目: 来源: 题型:
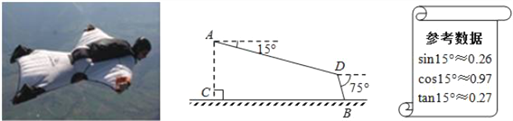
查看答案和解析>>【题目】如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形ABC中任意一点P(x0,y0)经平移后対应点为P1(x0+5,y0+3),将三角形ABC作同样的平移得到三角形A1B1C1,若A(﹣2,3),则A1的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于x和y的变量中(1)3x﹣2y=0,(2)y=|x|,(3)2x﹣y2=10,其中y是x的函数的是( )
A. (1) B. (1)(2) C. (2)(3) D. (1)(2)(3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形:平行四边形、矩形、菱形、圆、等腰三角形,这些图形中只是轴对称图形的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某储运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货物运往外地,这列货车持A.B两种类型的货厢共50节。已知甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,问:该储运站需配置A.B两种类型的货厢各几节?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(﹣2,﹣1),与y轴的交点为C,与x轴的交点为D.

(1)求一次函数解析式;
(2)求C点的坐标;
(3)求△AOD的面积.
相关试题

