【题目】已知等腰Rt△ABC中,∠BAC=90°.点D从点B出发沿射线BC移动,以AD为腰作等腰Rt△ADE,∠DAE=90°.连接CE.


(1)如图,求证:△ACE≌△ABD;
(2)点D运动时,∠BCE的度数是否发生变化?若不变化,求它的度数;若变化,说明理由;
(3)若AC=![]() ,当CD=1时,请求出DE的长.
,当CD=1时,请求出DE的长.
参考答案:
【答案】(1)见解析;(2)90°;(3)DE的长为![]() 或
或![]() .
.
【解析】试题分析:(1)由△ABC和△ADE都是等腰Rt△可得,AB=AC,AD=AE,∠BAC=∠DAE=90°,则有∠BAD=∠CAE,从而可证到△ACE≌△ABD;
(2)由△ACE≌△ABD可得∠ACE=∠ABD=45°,从而得到∠BCE=∠BCA+∠ACE=90°;
(3)可分点D在线段BC上时(如图1)和点D在线段BC延长线上时(如图2)两种情况讨论,在Rt△ABC中运用勾股定理可求出BC,从而得到BD,由△ACE≌△ABD可得CE=BD,在Rt△DCE中运用勾股定理就可求出DE.
试题解析:(1)∵△ABC和△ADE都是等腰Rt△,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ACE和△ABD中,
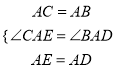 ,
,
∴△ACE≌△ABD;
(2)∵△ACE≌△ABD,
∴∠ACE=∠ABD=45°,
∴∠BCE=∠BCA+∠ACE=45°+45°=90°;
∴∠BCE的度数不变,为90°;
(3)①点D在线段BC上时,如图1,
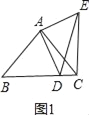
∵AB=AC=![]() ,∠BAC=90°,
,∠BAC=90°,
∴BC=![]() ,
,
∵CD=1,
∴BD=![]() ﹣1,
﹣1,
∵△ACE≌△ABD,
∴CE=BD=![]() ﹣1.
﹣1.
∵∠BCE=90°,
∴DE=![]() ;
;
②点D在线段BC延长线上时,如图2,
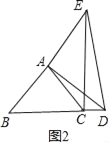
∵AB=AC=![]() ,∠BAC=90°,
,∠BAC=90°,
∴BC=![]() ,
,
∵CD=1,
∴BD=![]() +1,
+1,
∵△ACE≌△ABD,
∴CE=BD=![]() +1,
+1,
∵∠BCE=90°,
∴∠ECD=90°,
∴DE=![]() ,
,
综上所述:DE的长为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知:AB∥CD,点E,F分别在AB,CD上,且OE⊥OF.
(1)求证:∠1+∠2=90°;
(2)如图2,分别在OE,CD上取点G,H,使FO平分∠CFG,EO平分∠AEH,求证:FG∥EH.
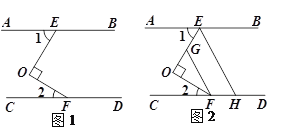
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,AB=AC,D 是直线 BC 上一点(不与点 B、C 重合),以 AD 为一边在 AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接 CE.
(1)如图 1,当点 D 在线段 BC 上时,求证:△ABD≌△ACE;
(2)如图 2,当点 D 在线段 BC 上时,如果∠BAC=90°,求∠BCE 的度数;
(3)如图 3,若∠BAC=α,∠BCE=β.点 D 在线段 CB 的延长线上时,则α、β之间有怎样 的数量关系?并证明你的结论.



-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,长方形 ABCD 中,AB=3cm,BC=6cm,P 为矩形 ABCD 上的动点,动点 P 从 A 出发,沿着 A-B-C-D 运动到 D 点停止,速度为 1cm/s,设点 P 运动时间为 x 秒,△APD 的面积为 ycm.
(1)填空:①当 x=6 时,对应 y 的值为________;9≤x<12 时,y 与 x 之间的关系式为_____;
(2)当 y=3 时,求 x 的值;
(3)当 P 在线段 BC 上运动时,是否存在点 P 使得△APD 的周长最小?若存在,求出此时∠APD 的度数;若不存在,请说明理由.

图1
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作探究:
数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图1所示的长方形纸条ABCD,其中AD=BC=1,AB=CD=5.然后在纸条上任意画一条截线段MN,将纸片沿MN折叠,MB与DN交于点K,得到△MNK.如图2所示:

探究:
(1)若∠1=70°,∠MKN= °;
(2)改变折痕MN位置,△MNK始终是 三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究△MNK的面积时,发现KN边上的高始终是个不变的值.根据这一发现,他很快研究出△KMN的面积最小值为
 ,此时∠1的大小可以为 °
,此时∠1的大小可以为 °(4)小明继续动手操作,发现了△MNK面积的最大值.请你求出这个最大值.

-
科目: 来源: 题型:
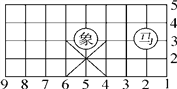
查看答案和解析>>【题目】如图是中国象棋棋盘的一部分,棋盘中“马”所在的位置用(2,3)表示.
(1)图中“象”的位置可表示为____________;
(2)根据象棋的走子规则,“马”只能从“日”字的一角走到与它相对的另一角;“象”只能从“田”字的一角走到与它相对的另一角.请按此规则分别写出“马”和“象”下一步可以到达的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
相关试题

