【题目】如图 1,长方形 ABCD 中,AB=3cm,BC=6cm,P 为矩形 ABCD 上的动点,动点 P 从 A 出发,沿着 A-B-C-D 运动到 D 点停止,速度为 1cm/s,设点 P 运动时间为 x 秒,△APD 的面积为 ycm.
(1)填空:①当 x=6 时,对应 y 的值为________;9≤x<12 时,y 与 x 之间的关系式为_____;
(2)当 y=3 时,求 x 的值;
(3)当 P 在线段 BC 上运动时,是否存在点 P 使得△APD 的周长最小?若存在,求出此时∠APD 的度数;若不存在,请说明理由.

图1
参考答案:
【答案】 9 y=-3x+36
【解析】(1)利用三角形面积求法S△APD=![]() 即可得出答案;当9<x≤12时,点P运动到CD边上,S△APD=
即可得出答案;当9<x≤12时,点P运动到CD边上,S△APD=![]() 得出y与x的函数关系式即可;
得出y与x的函数关系式即可;
(2)分别求出点P在AB、BC、CD上y与x的函数关系式,利用y=3,求出x的值即可;
(3)利用轴对称求最短路线的方法得出P点位置,进而利用全等三角形的性质求出答案.
(1)9;y=-3x+36;
(2)当 P 从 A-B 运动时,y=3x;当 P 从 B-C 运动时,y=9;当 P 从 C-D 运动时,y=-3x+36;令 y=3,则 3x=3 或-3x+36=3,解得 x=1 或 11.
(3)存在.理由:如图,延长 DC,使得 DC=D’C,连接 AD’,交 BC 于点 P,则 P 为所求,

且△PCD≌△PCD’,
∴PD=PD’,∠PCD=∠PCD’ 因为四边形 ABCD 是长方形
∴AB=CD,∠B=∠PCD=90°
∴AB=CD’,∠PCD’=90°
在△ABP 与△D’CP 中,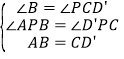
∴△ABP≌△D’CP(AAS)
∴BP PC![]() BC3,
BC3,
∵AB=DC=3,
∴AB=BP,PC=CD,
∴∠APB=∠BAP=45°,∠DPC=∠DPC=45°,
∵∠APB+∠APD+∠CPD=180°,
∴∠APD=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知:AB∥CD,点E,F分别在AB,CD上,且OE⊥OF.
(1)求证:∠1+∠2=90°;
(2)如图2,分别在OE,CD上取点G,H,使FO平分∠CFG,EO平分∠AEH,求证:FG∥EH.
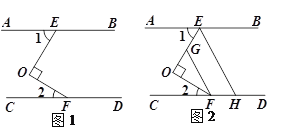
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,AB=AC,D 是直线 BC 上一点(不与点 B、C 重合),以 AD 为一边在 AD的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接 CE.
(1)如图 1,当点 D 在线段 BC 上时,求证:△ABD≌△ACE;
(2)如图 2,当点 D 在线段 BC 上时,如果∠BAC=90°,求∠BCE 的度数;
(3)如图 3,若∠BAC=α,∠BCE=β.点 D 在线段 CB 的延长线上时,则α、β之间有怎样 的数量关系?并证明你的结论.



-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰Rt△ABC中,∠BAC=90°.点D从点B出发沿射线BC移动,以AD为腰作等腰Rt△ADE,∠DAE=90°.连接CE.


(1)如图,求证:△ACE≌△ABD;
(2)点D运动时,∠BCE的度数是否发生变化?若不变化,求它的度数;若变化,说明理由;
(3)若AC=
 ,当CD=1时,请求出DE的长.
,当CD=1时,请求出DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】操作探究:
数学研究课上,老师带领大家探究《折纸中的数学问题》时,出示如图1所示的长方形纸条ABCD,其中AD=BC=1,AB=CD=5.然后在纸条上任意画一条截线段MN,将纸片沿MN折叠,MB与DN交于点K,得到△MNK.如图2所示:

探究:
(1)若∠1=70°,∠MKN= °;
(2)改变折痕MN位置,△MNK始终是 三角形,请说明理由;
应用:
(3)爱动脑筋的小明在研究△MNK的面积时,发现KN边上的高始终是个不变的值.根据这一发现,他很快研究出△KMN的面积最小值为
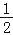 ,此时∠1的大小可以为 °
,此时∠1的大小可以为 °(4)小明继续动手操作,发现了△MNK面积的最大值.请你求出这个最大值.

-
科目: 来源: 题型:
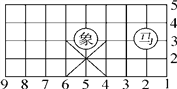
查看答案和解析>>【题目】如图是中国象棋棋盘的一部分,棋盘中“马”所在的位置用(2,3)表示.
(1)图中“象”的位置可表示为____________;
(2)根据象棋的走子规则,“马”只能从“日”字的一角走到与它相对的另一角;“象”只能从“田”字的一角走到与它相对的另一角.请按此规则分别写出“马”和“象”下一步可以到达的位置.
相关试题

