【题目】已知△ABC的面积是60,请完成下列问题:
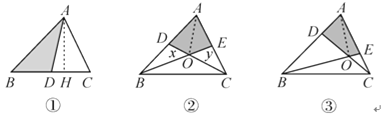
(1)如图①,若AD是△ABC的BC边上的中线,则△ABD的面积 _△ACD的面积(选填“>”“<”或“=”).
(2)如图②,若CD,BE分别是△ABC的AB,AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO,同理:S△CEO=S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y,由题意得:S△ABE=![]() S△ABC=30,S△ADC=
S△ABC=30,S△ADC=![]() S△ABC=30,可列方程组为: ,通过解这个方程组可得四边形ADOE的面积为 .
S△ABC=30,可列方程组为: ,通过解这个方程组可得四边形ADOE的面积为 .
(3)如图③,AD∶DB=1∶3,CE∶AE=1∶2,请你计算四边形ADOE的面积,并说明理由.

参考答案:
【答案】(1)=;(2)![]() ,20;(3)S四边形ADOE=13.
,20;(3)S四边形ADOE=13.
【解析】(1)如图1,过A作AH⊥BC于H,根据等底等高的两个三角形面积相等知,三角形的中线把三角形的面积分为相等的两部分,所以S△ABD=S△ACD;
(2)根据三角形的中线能把三角形的面积平分,等高三角形的面积的比等于底的比,即可得到结果;
(3)连结AO,由AD:DB=1:3,得到S△ADO=![]() S△BDO,同理可得S△CEO=
S△BDO,同理可得S△CEO=![]() S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=3x,S△AEO=2y,由题意得列方程组即可得到结果.
S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=3x,S△AEO=2y,由题意得列方程组即可得到结果.
(1)如图1,过A作AH⊥BC于H,
∵AD是△ABC的BC边上的中线,
∴BD=CD,∴S△ABD=![]() BD·AH,
BD·AH,
S△ACD=![]() CD·AH,∴S△ABD=S△ACD;
CD·AH,∴S△ABD=S△ACD;
(2)列方程组![]() 解方程组得
解方程组得![]()
∴S△AOD=S△BOD=10,∴S四边形ADOE=S△AOD+S△AOE=10+10=20;
(3)如图3,连接AO,∵AD∶DB=1∶3,
∴S△ADO=![]() S△BDO,∵CE∶AE=1∶2,
S△BDO,∵CE∶AE=1∶2,
∴S△CEO=![]() S△AEO,
S△AEO,
设S△ADO=x,S△CEO=y,则S△BDO=3x,S△AEO=2y,
由题意得:S△ABE=![]() S△ABC=40,S△ADC=
S△ABC=40,S△ADC=![]() S△ABC=15,
S△ABC=15,
可列方程组为![]() 解得
解得![]()
∴S四边形ADOE=S△ADO+S△AEO=x+2y=13.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图.则在字母L,K,C的投影中,与字母N属同一种投影的有( )

A.L,K
B.C
C.K
D.L,K,C -
科目: 来源: 题型:
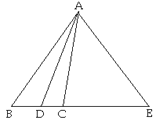
查看答案和解析>>【题目】如图,AD平分∠BAC,∠EAD=∠EDA.
(1)∠EAC与∠B相等吗?为什么?
(2)若∠B=50°,∠CAD︰∠E=1︰3,求∠E的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店,甲种笔记本标价每本8元,乙种笔记本标价每本5元
(1)两种笔记本各销售了多少?
(2)所得销售款可能是660元吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G.点F是CD上一点,且满足
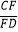 =
=  ,连接AF并延长交⊙0于点E.连接AD,DE,若CF=2,AF=3.给出下列结论:
,连接AF并延长交⊙0于点E.连接AD,DE,若CF=2,AF=3.给出下列结论:
①△ADF∽△AED;②FG=2;③tan∠E=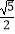 ;④S△DEF=4
;④S△DEF=4 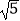 .
.
其中正确的是( )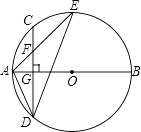
A.①②④
B.①②③
C.②③④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )
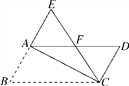
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏为了解本市的空气质量情况,从市环保局随机抽取了若干天的空气质量情况作为标本进行统计,绘制成如图所示的条形统计图和扇形统计图(部分信息为给出)
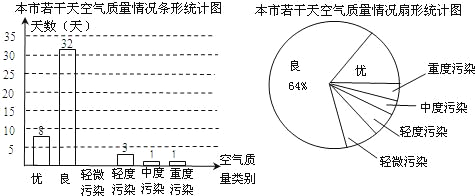
请你根据图中提供的信息,解答下列问题:
(1)本次调查中共抽取了多少天的空气质量情况作为标本?
(2)求轻微污染天数并补全条形统计图;
(3)请你估计该市这一年(365天)空气质量达到“优”和“良”的总天数.
相关试题

