【题目】教材第九章中探索乘法公式时,设置由图形面积的不同表示方法验证了乘法公式.我国著名的数学家赵爽,早在公元3世纪,就把一个矩形分成四个全等的直角三角形,用四个全等的直角三角形拼成了一个大的正方形(如图①),这个图形称为赵爽弦图,验证了一个非常重要的结论:在直角三角形中两直角边a、b与斜边c满足关系式a2+b2=c2,称为勾股定理.
(1)爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形(如图②),也能验证这个结论,请你帮助小明完成验证的过程.
(2)小明又把这四个全等的直角三角形拼成了一个梯形(如图③),利用上面探究所得结论,求当a=3,b=4时梯形ABCD的周长.
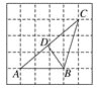
(3)如图④,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.请在图中画出△ABC的高BD,利用上面的结论,求高BD的长.


参考答案:
【答案】(1)根据题意,我们可在图中找等量关系,由中间的小正方形的面积等于大正方形的面积减去四个直角三角形的面积,列出等式化简即可得出勾股定理的表达式;(2)![]() ;(3)作出高BD如下图,BD=
;(3)作出高BD如下图,BD=![]()

【解析】
(1)根据四个全等的直角三角形的面积+阴影部分小正方形的面积=大正方形的面积,代入数值,即可证明;
(2)由(1)中结论先求出c的值,再根据周长公式即可得出梯形ABCD的周长;
(3)先根据高的定义画出BD,由(1)中结论求出AC的长,再根据△ABC的面积不变列式,即可求出高BD的长.
(1)证明 由图得,![]() ×ab×4+c2=(a+b)×(a+b),
×ab×4+c2=(a+b)×(a+b),
整理,得2ab+c2=a2+b2+2ab,
即a2+b2=c2;
(2)解 ∵a=3,b=4,
∴c=![]() =5,
=5,
梯形ABCD的周长为:a+c+3a+c=4a+2c=4×3+2×5=22;
(3)解 如图4,BD是△ABC的高.
∵S△ABC=![]() AC·BD=
AC·BD=![]() AB×3,AC=
AB×3,AC=![]() =5,
=5,
∴BD=![]() =
=![]() =
=![]() .
.
故答案为:(1)见解析;(2)22;(3)![]() .
.
-
科目: 来源: 题型:
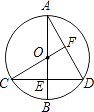
查看答案和解析>>【题目】在⊙O中,直径AB⊥CD于点E,连接CO并延长交AD于点F,且CF⊥AD.求∠D的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,AB=4cm,线段AB上一动点D,以1cm/s的速度从点A出发向终点B运动.过点D作DE⊥AB,交折线AC﹣CB于点E,以DE为一边,在DE左侧作正方形DEFG.设运动时间为x(s)(0<x<4).正方形DEFG与△ABC重叠部分面积为y(cm2).

(1)当x=s时,点F在AC上;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
(3)设正方形DEFG的中心为点O,直接写出运动过程中,直线BO平分△ABC面积时,自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,池塘边有一块长为18m,宽为10m的长方形土地,现在将其 余三面留出宽都是xm的小路,中间余下的长方形部分做菜地,用整式表示:
(1)菜地的长a= m,宽b= m;
(2)菜地面积S= m2;
(3)当x=0.5m时,菜地面积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在实数范围内定义一种运算“*”,其运算法则为a*b=a2﹣ab.根据这个法则,下列结论中正确的是_______.(把所有正确结论的序号都填在横线上)
①
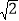 *
* =2﹣
=2﹣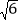 ;②若a+b=0,则a*b=b*a;③(x+2)*(x+1)=0是一元二次方程;④方程(x+3)*1=1的根是x1=
;②若a+b=0,则a*b=b*a;③(x+2)*(x+1)=0是一元二次方程;④方程(x+3)*1=1的根是x1=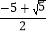 ,x2=
,x2=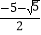 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】七年级学生在5 名教师的带领下去动物园秋游,动物园的门票为每 人40 元,现有两种优惠方案,甲方案:带队教师免费,学生按8 折收费;乙 方案:师生都7.5 折收费.
(1)若有m 名学生,用含m 的式子表示两种优惠方案各需多少元?
(2)当m=70 时,采用哪种方案优惠?
(3)当m=100 时,采用哪种方案优惠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中的两点A(m,0),B(2m,0)(m>0),二次函数y=ax2+bx+m的图象与x轴交与A,B两点与y轴交于点C,顶点为点D.
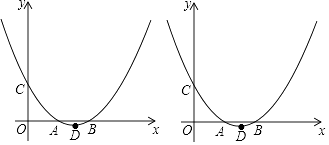
(1)当m=1时,直线BC的解析式为 , 二次函数y=ax2+bx+m的解析式为;
(2)求二次函数y=ax2+bx+m的解析式为(用含m的式子表示);
(3)连接AC、AD、BD,请你探究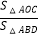 的值是否与m有关?若有关,求出它与m的关系;若无关,说明理由;
的值是否与m有关?若有关,求出它与m的关系;若无关,说明理由;
(4)当m为正整数时,依次得到点A1 , A2 , …,Am的横坐标分别为1,2,…m;点B1 , B2 , …,Bm 的横坐标分别为2,4,…2m(m≤10);经过点A1 , B1 , 点A2 , B2 , …,点Am , Bm的这组抛物线y=ax2+bx+m分别与y轴交于点C1 , C2 , …,Cm , 由此得到了一组直线B1C1 , B2C2 , …,BmCm , 在点B1 , B2 , …,Bm 中任取一点Bn , 以线段OBn为边向上作正方形OBnEnFn , 若点En在这组直线中的一条直线上,直接写出所有满足条件的点En的坐标.
相关试题

