【题目】如图,二次函数y=![]() x2+bx﹣
x2+bx﹣![]() 的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.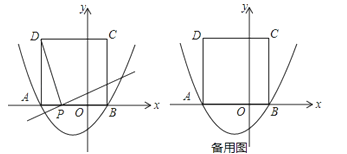
(1)b的值及点D的坐标。
(2)线段AO上是否存在点P(点P不与A、O重合),使得OE的长为1;
(3)在x轴负半轴上是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
参考答案:
【答案】解:(1)∵点A(﹣3,0)在二次函数y=![]() x2+bx﹣
x2+bx﹣![]() 的图象上,
的图象上,
∴0=![]() ﹣3b﹣
﹣3b﹣![]() ,解得b=1,
,解得b=1,
∴二次函数解析式为y=![]() x2+x﹣
x2+x﹣![]() =
=![]() (x+3)(x﹣1),
(x+3)(x﹣1),
∴点B(1,0),AB=1﹣(﹣3)=4,
∵四边形ABCD为正方形,
∴AD=AB=4,
∴点D(﹣3,4),
故答案为:1;(﹣3,4).
(2)直线PE交y轴于点E,如图1,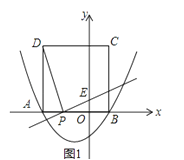
假设存在点P,使得OE的长为1,设OP=a,则AP=3﹣a,
∵DP⊥AE,∠APD+∠DPE+∠EPO=180°,
∴∠EPO=90°﹣∠APD=∠ADP,
tan∠ADP=![]() =
=![]() ,tan∠EPO=
,tan∠EPO=![]() =
=![]() ,
,
∴![]() =
=![]() ,即a2﹣3a+4=0,
,即a2﹣3a+4=0,
△=(﹣3)2﹣4×4=﹣7,无解
故线段AO上不存在点P(点P不与A、O重合),使得OE的长为1.
(3)假设存在这样的点P,DE交x轴于点M,如图2,
∵△PED是等腰三角形,
∴DP=PE,
∵DP⊥PE,四边形ABCD为正方形
∴∠EPO+∠APD=90°,∠DAP=90°,∠PAD+∠APD=90°,
∴∠EPO=∠PDA,∠PEO=∠DPA,
在△PEO和△DAP中,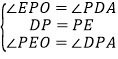 ,
,
∴△PEO≌△DAP,
∴PO=DA=4,OE=AP=PO﹣AO=4﹣3=1,
∴点P坐标为(﹣4,0).
∵DA⊥x轴,
∴DA∥EO,
∴∠ADM=∠OEM(两直线平行,内错角相等),
又∵∠AMD=∠OME(对顶角),
∴△DAM∽EOM,
∴![]() =
=![]() =
=![]() ,
,
∵OM+MA=OA=3,
∴MA=![]() ×3=
×3=![]() ,
,
△PED与正方形ABCD重叠部分△ADM面积为![]() ×AD×AM=
×AD×AM=![]() ×4×
×4×![]() =
=![]() .
.
答:存在这样的点P,点P的坐标为(﹣4,1),此时△PED与正方形ABCD重叠部分的面积为![]() .
.
【解析】(1)利用点在二次函数图象上,代入即可求得b,将二次函数换成交点式,即能得出B点的坐标,由AD=AB可算出D点坐标;
(2)假设存在,由DP⊥AE,找出∠EPO=∠PDA,利用等角的正切相等,可得出一个关于OP长度的一元二次方程,由方程无解可得知不存在这样的点;
(3)利用角和边的关系,找到全等,再利用三角形相似,借助相似比即可求得AM,求出△ADM的面积即是所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果经过三角形某一个顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形的生成三角形,简称生成三角形.
(1)如图,已知等腰直角三角形ABC,∠A=90°,试说明:△ABC是生成三角形;
(2)若等腰三角形DEF有一个内角等于36°,请你画出简图说明△DEF是生成三角形.(要求画出直线,标注出图中等腰三角形的顶角、底角的度数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB,按下列要求完成画图和计算:
(1)延长线段AB到点C,使BC=2AB,取AC中点D;
(2)在(1)的条件下,如果AB=4,求线段BD的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC=10 cm,AB=12 cm,点D是AB的中点,连结CD,动点P从点A出发,沿A→C→B的路径运动,到达点B时运动停止,速度为每秒2 cm,设运动时间为
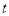 秒.
秒.(1)求CD的长;
(2)当
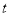 为何值时,△ADP是直角三角形?
为何值时,△ADP是直角三角形?(3)直接写出:当
 为何值时,△ADP是等腰三角形?
为何值时,△ADP是等腰三角形?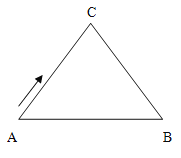
-
科目: 来源: 题型:
查看答案和解析>>【题目】“珍惜生命,注意安全”是一永恒的话题.在现代化的城市,交通安全晚不能被忽视,下列几个图形是国际通用的几种交通标志,其中不是中心对称图形是( )
A.禁止行车
B.禁止行人通行
C.禁止车辆长时间停放
D.禁止车辆临时或长时间停放
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,若sinA=
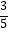 , 则cosB的值是( )
, 则cosB的值是( )
A.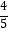
B.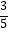
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB,点P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点.
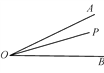
(1)要使得△PEF的周长最小,试在图上确定点E、F的位置.
(2)若OP=4,要使得△PEF的周长的最小值为4,则∠AOB=________.
相关试题

