【题目】某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
![]()
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求该机器的生产数量;
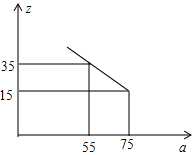
(3)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器40台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价-成本)
参考答案:
【答案】(1) y=-![]() x+65.10≤x≤70;(2) 50台;(3) 312.5万元.
x+65.10≤x≤70;(2) 50台;(3) 312.5万元.
【解析】
试题分析:(1)设y与x之间的关系式为y=kx+b,运用待定系数法就可以求出其关系式,由该机器生产数量至少为10台,但不超过70台就可以确定自变量的取值范围;
(2)根据每台的成本乘以生产数量等于总成本建立方程求出其解即可;
(3)设每月销售量z(台)与售价a(万元∕台)之间的函数关系式为z=ma+n,运用待定系数法求出其解析式,再将z=25代入解析式求出a的值,就可以求出每台的利润,从而求出总利润.
试题解析:(1)设y与x之间的关系式为y=kx+b,由题意,得
![]() ,
,
解得: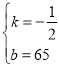 ,
,
∴y=-![]() x+65.
x+65.
∵该机器生产数量至少为10台,但不超过70台,
∴10≤x≤70;
(2)由题意,得
xy=2000,
-![]() x2+65x=2000,
x2+65x=2000,
-x2+130x-4000=0,
解得:x1=50,x2=80>70(舍去).
答:该机器的生产数量为50台;
(3)设每月销售量z(台)与售价a(万元∕台)之间的函数关系式为z=ma+n,由函数图象,得
![]() ,
,
解得:![]() ,
,
∴z=-a+90.
当z=25时,a=65,
成本y=-![]() z+65=-
z+65=-![]() ×25+65=
×25+65=![]() (万元);
(万元);
总利润为:25(65-![]() )=
)=![]() =312.5(万元).
=312.5(万元).
答:该厂第一个月销售这种机器的利润为312.5万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x-1≥3x-3的正整数解的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( ).
A. 不等式x-3>2的解集是x>5 B. 不等式x<3的整数解有无数个
C. x=0是不等式2x<3的一个解 D. 不等式x+3<3的整数解是0
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程,并解答后面的问题:如图1,在平面直角坐标系
 中,
中, ,
, ,
, 为线段
为线段 的中点,求
的中点,求 点的坐标.
点的坐标.解:分别过
 、
、 作
作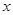 轴的平行线,过
轴的平行线,过 、
、 作
作 轴的平行线,两组平行线的交点如图1所示.
轴的平行线,两组平行线的交点如图1所示.设
 ,则
,则 ,
, ,
,
由图1可知:


∴

问题:
(1)已知
 ,
, ,
, ,
, ,则线段
,则线段 的中点坐标为 ;
的中点坐标为 ;(2)□
 中,点
中,点 、
、 、
、 的坐标分别为
的坐标分别为 ,
, ,
, ,
, ,
, ,
, ,求点
,求点 的坐标;
的坐标;(3)如图2,点
 ,
, 与点
与点 在函数
在函数 的图像上,点
的图像上,点 ,
, ,点
,点 在
在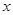 轴上,以
轴上,以 、
、 、
、 、
、 四个点为顶点构成平行四边形,请你直接写出所有满足条件的
四个点为顶点构成平行四边形,请你直接写出所有满足条件的 点坐标.
点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在抗震救灾中,某抢险地段需实行爆破.操作人员点燃导火线后,要在炸药爆炸前跑到400米以外的安全区域.已知导火线的燃烧速度是1.2厘米/秒,操作人员跑步的速度是5米/秒.为了保证操作人员的安全,导火线的长度要超过( )
A. 66厘米 B. 76厘米 C. 86厘米 D. 96厘米
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面上一个菱形绕它的中心旋转,使它和原来的菱形重合,那么旋转的角度至少是( )
A.180°
B.90°
C.270°
D.360° -
科目: 来源: 题型:
查看答案和解析>>【题目】关于某一点成中心对称的两个图形,它们的对称点的连线都经过 , 并且被平分.
相关试题

