【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=(x-1)2-4,AB为半圆的直径,求这个“果圆”被y轴截得的弦CD的长 . 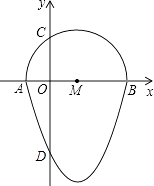
参考答案:
【答案】 ![]()
【解析】连接AC,BC,
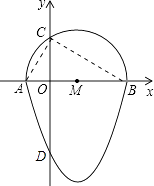
∵抛物线的解析式为y=(x-1)2-4,
∴点D的坐标为(0,3),
∴OD的长为3,
设y=0,则0=(x-1)2-4,
解得:x=1或3,
∴A(1,0),B(3,0)
∴AO=1,BO=3,
∵AB为半圆的直径,
∴∠ACB=90°,
∵CO⊥AB,
∴CO2=AOBO=3,
∴CO= ![]() ,
,
∴CD=CO+OD=3+ ![]() ,
,
所以答案是:3+ ![]() .
.
【考点精析】利用二次函数的性质和抛物线与坐标轴的交点对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知长方形ABCO中,边AB=12,BC=8.以点0为原点,OA、OC所在的直线为y轴和x轴建立直角坐标系.
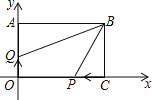
(1)点A的坐标为(0,8),写出B.C两点的坐标;
(2)若点P从C点出发,以3单位/秒的速度向CO方向移动(不超过点O),点Q从原点O出发,以2单位/秒的速度向OA方向移动(不超过点A),设P、Q两点同时出发,在它们移动过程中,四边形OPBQ的面积是否发生变化?若不变,求其值;若变化,求变化范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知表示实数a,b的点在数轴上的位置如图所示,下列结论错误的是( )
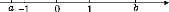
A.
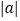 <1<
<1<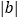 B. 1<-a<b C. 1<
B. 1<-a<b C. 1<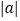 <b D. -b<a<-1
<b D. -b<a<-1 -
科目: 来源: 题型:
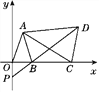
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且|a+b-3|+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数
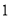 至
至 按照一定规律排成下表:
按照一定规律排成下表: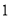
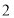


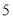

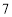
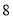


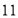

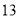
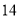
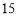
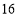






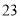



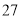
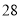
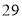


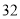
……
记
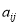 表示第
表示第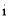 行第
行第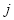 个数,如
个数,如 表示第
表示第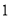 行第
行第 个数是
个数是 .
.(1)直接写出
 _______________,
_______________, _______________;
_______________;(2)①如果
 ,那么
,那么 _________________,
_________________,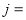 ________;②用
________;②用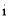 ,
,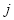 表示
表示 __________;
__________;(3)将表格中的
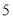 个阴影格子看成一个整体并平移,所覆盖的
个阴影格子看成一个整体并平移,所覆盖的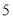 个数之和能否等于
个数之和能否等于 .若能,求出这
.若能,求出这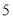 个数中的最小数,若不能说明理由.
个数中的最小数,若不能说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AC的表达式为y=
 x+8,点P从点A开始沿AO向点O以1个单位/s的速度移动,点Q从点O开始沿OC向点C以2个单位/s的速度移动.如果P,Q两点分别从点A,O同时出发,经过几秒能使△PQO的面积为8个平方单位?
x+8,点P从点A开始沿AO向点O以1个单位/s的速度移动,点Q从点O开始沿OC向点C以2个单位/s的速度移动.如果P,Q两点分别从点A,O同时出发,经过几秒能使△PQO的面积为8个平方单位?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行于x轴的直线AC分别交抛物线
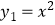 (x≥0)与
(x≥0)与 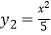 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 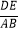 = .
= . 
相关试题

