搜索
【题目】如图，已知长方形ABCO中，边AB=12，BC=8．以点0为原点，OA、OC所在的直线为y轴和x轴建立直角坐标系．
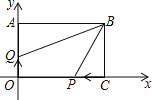
（1）点A的坐标为（0，8），写出B．C两点的坐标；
（2）若点P从C点出发，以3单位/秒的速度向CO方向移动（不超过点O），点Q从原点O出发，以2单位/秒的速度向OA方向移动（不超过点A），设P、Q两点同时出发，在它们移动过程中，四边形OPBQ的面积是否发生变化?若不变，求其值；若变化，求变化范围．
参考答案：
【答案】（1）
；（2）四边形OPBQ的面积不会发生变化，其值始终为48．
【解析】
（1）根据长方形的性质可知
，从而即可确定B,C的坐标；
（2）设P,Q运动时间为t，分别用含t的代数式表示出
，最后利用
即可得出答案．
（1）∵四边形ABCO是长方形，
∴．
∵
，
；
（2）四边形OPBQ的面积不会发生变化，理由如下：
设P,Q运动时间为t，则
，
，
∴
，
，
∴
，
∴四边形OPBQ的面积不会发生变化，其值始终为48．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直角坐标系中，△ABC的顶点都在网格点上，其中C点坐标为（1，2），
（1）请画出△ABC向左平移1个单位长度，再向上平移2个单位长度后的△A′B′C′，（其中A′、B′、C′分别是A、B、C的对应点）
（2）直接写出A′、B′、C′三点的坐标：A′（_____，______）；B′（_____，______）；C′（_____，______）．
（3）△ABC的面积为______________平方单位
-
科目： 来源： 题型：
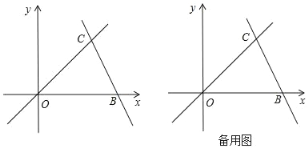
查看答案和解析>>【题目】如图，直线OC、BC的函数关系式分别为y＝x和y＝﹣2x+b，且交点C的横坐标为2，动点P（x，0）在线段OB上移动（0＜x＜3）．
（1）求点C的坐标和b；
（2）若点A（0，1），当x为何值时，AP+CP的值最小；
（3）过点P作直线EF⊥x轴，分别交直线OC、BC于点E、F．
①若EF＝3，求点P的坐标．
②设△OBC中位于直线EF左侧部分的面积为s，请写出s与x之间的函数关系式，并写出自变量的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，AB∥DE，AC∥DF，AC=DF下列条件中，不能判断△ABC≌△DEF的是（ ）
A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知表示实数a，b的点在数轴上的位置如图所示，下列结论错误的是( )
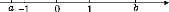
A.
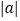＜1＜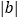
B. 1＜－a＜b C. 1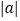＜＜b D. －b＜a＜－1 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知点A(a－1，a＋b)，B(a，0)，且|a＋b－3|＋(a－2b)2＝0，C为x轴上点B右侧的动点，以AC为腰作等腰三角形ACD，使AD＝AC，∠CAD＝∠OAB，直线DB交y轴于点P.
(1)求证：AO＝AB；
(2)求证：△AOC≌△ABD；
(3)当点C运动时，点P在y轴上的位置是否发生改变，为什么？
-
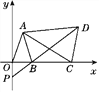
科目： 来源： 题型：
查看答案和解析>>【题目】如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”．已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=(x-1)2-4，AB为半圆的直径，求这个“果圆”被y轴截得的弦CD的长 ．
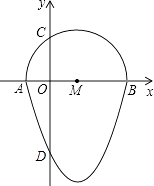
相关试题
