【题目】在△ABC中,AB=BC,∠ABC=90°.以AB为斜边作等腰直角三角形ADB.点P是直线DB上一个动点,连接AP,作PE⊥AP交BC所在的直线于点E.

(1)如图1,点P在BD的延长线上,PE⊥EC,AD=1,直接写出PE的长;
(2)点P在线段BD上(不与B,D重合),依题意,将图2补全,求证:PA=PE;
(3)点P在DB的延长线上,依题意,将图3补全,并判断PA=PE是否仍然成立.
参考答案:
【答案】(1)![]() ; (2)证明见解析;(3)证明见解析.
; (2)证明见解析;(3)证明见解析.
【解析】
(1)根据等腰直角三角形的性质得到∠ABP=45°,根据勾股定理得到AB=![]() =
=![]() ,推出四边形ABEP是矩形,得到四边形ABEP是正方形,于是得到结论;(2)根据等腰直角三角形的性质得到∠ADB=90°,∠DAB=∠DBA=45°,求得∠PBN=45°过P作PM⊥AB于点M,过P作PN⊥BC于点N,于是得到PM=PN,∠BPN=45°根据全等三角形的性质即可得到结论;
,推出四边形ABEP是矩形,得到四边形ABEP是正方形,于是得到结论;(2)根据等腰直角三角形的性质得到∠ADB=90°,∠DAB=∠DBA=45°,求得∠PBN=45°过P作PM⊥AB于点M,过P作PN⊥BC于点N,于是得到PM=PN,∠BPN=45°根据全等三角形的性质即可得到结论;
(3)根据等腰直角三角形的性质得到∠ABD=45°,得到∠PBN=45°,∠ABC=90°,过P作PM⊥AB于点M,过P作PN⊥BC于点N,得到四边形BMPN是矩形,推出四边形BMPN是正方形,得到PM=PN,根据全等三角形的性质即可得到结论.
(1)∵AD=DB=1,∠ADB=90°,
∴∠ABP=45°,AB=![]() =
=![]() ,
,
∵PE⊥AP,AB⊥BC,
∴PA∥EC,
∴PA⊥AB,
∴四边形ABEP是矩形,
∵∠ABP=45°,
∴PA=AB,
∴四边形ABEP是正方形,
∴PE=AB=![]()
(2)∵△ABC和△ADB是等腰直角三角形,
∴∠ADB=90°,∠DAB=∠DBA=45°,
∴∠PBN=45°
∴PE⊥AP,∠DAP=∠BPE=90°-∠DPA,
∵∠PAM=45°-∠DAP,∠PEN=45°-∠BPE,
∴∠PAM=∠PEN,
过P作PM⊥AB于点M,过P作PN⊥BC于点N,

则PM=PN,∠BPN=45°,
在△APM和△EPN中,
 ,
,
∴△APM≌△EPN,
∴PA=PE;
(3)∵△ABC和△ADB是等腰直角三角形,
∴∠ABD=45°,
∴∠PBN=45°,∠ABC=90°,
过P作PM⊥AB于点M,过P作PN⊥BC于点N,

则四边形BMPN是矩形,
∵∠NBP=45°,
∴四边形BMPN是正方形,
∴PM=PN,
∵AB⊥BC,
∴∠BAN=∠APN,
∵AP⊥PE,
∴∠APN=∠E,
∴∠BAP=∠E,
在△AMP与△ENP中,
 ,
,
∴△AMP≌△ENP,
∴AP=PE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】创建文明城市,人人参与,人人共建.我市各校积极参与创建活动,自发组织学生走上街头,开展文明劝导活动.某中学九(一)班为此次活动制作了大小、形状、质地等都相同的“文明劝导员”胸章和“文明监督岗”胸章若干,放入不透明的盒中,此时从盒中随机取出“文明劝导员”胸章的概率为
 ;若班长从盒中取出“文明劝导员”胸章3只、“文明监督岗”胸章7只送给九(二)班后,这时随机取出“文明劝导员”胸章的概率为
;若班长从盒中取出“文明劝导员”胸章3只、“文明监督岗”胸章7只送给九(二)班后,这时随机取出“文明劝导员”胸章的概率为  .
.
(1)请你用所学知识计算:九(一)班制作的“文明劝导员”胸章和“文明监督岗”胸章各有多少只?
(2)若小明一次从盒内剩余胸章中任取2只,问恰有“文明劝导员”胸章、“文明监督岗”胸章各1只的概率是多少?(用列表法或树状图计算) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8)、动点M、N分别从O、B同时出发,都以每秒1个单位的速度运动、其中,点M沿OA向终点A运动,点N沿BC向终点C运动、过点N作NP⊥BC,交AC于P,连结MP、已知动点运动了t秒、

(1)P点的坐标为( , )(用含t的代数式表示);
(2)试求 △MPA面积的最大值,并求此时t的值;
(3)请你探索:当t为何值时,△MPA是一个等腰三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:抛物线y=-
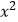 +bx+c与x轴交于A、B两点,与y轴交于点C,且∠BAC=α,∠ABC=
+bx+c与x轴交于A、B两点,与y轴交于点C,且∠BAC=α,∠ABC= 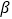 ,tanα-tanβ=2,∠ACB=90°.
,tanα-tanβ=2,∠ACB=90°.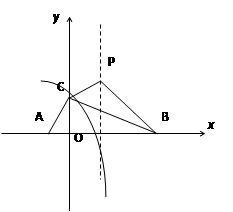
(1)求点C的坐标;
(2)求抛物线的解析式;
(3)若抛物线的顶点为P,求四边形ABPC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列银行标志,从图案看既是轴对称图形又是中心对称图形的有( )




A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】小彬买了A、B两种书,单价分别是18元、10元.
(1)若两种书共买了10本付款172元,求每种书各买了多少本?
(2)买10本时付款可能是123元吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在质地和颜色都相同的三张卡片的正面分别写有-2,-1,1,将三张卡片背面朝上洗匀,从中抽出一张,并记为x,然后从余下的两张中再抽出一张,记为y, 则点(x,y)在反比例函数y=

 图象上的概率为( )
图象上的概率为( )
A.
B.

C.

D.1
相关试题

