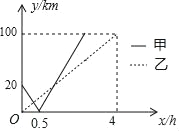
【题目】沿河岸有A,B,C三个港口,甲乙两船同时分别从AB港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:
①乙船的速度是25km/h;②从A港到C港全程为120km;③甲船比乙船早1.5小时到达终点;④若设图中两者相遇的交点为P点,P点的坐标为(![]() ,
,![]() );⑤如果两船相距小于10km能够相互望见,那么甲、乙两船可以相互望见时,x的取值范围是
);⑤如果两船相距小于10km能够相互望见,那么甲、乙两船可以相互望见时,x的取值范围是![]() <x<2.其中正确的结论有_____.
<x<2.其中正确的结论有_____.
参考答案:
【答案】①②
【解析】分析:由速度=路程÷时间,可知甲、乙两船的速度,由此可判断①成立;结合图形中甲的图象可知,A、C两港距离=20+100=120km,由此可判断②成立;由时间=路程÷速度可知甲、乙两船到达C港的时间,由此可判断③不成立;由A港口比B港口离C港口多20km,结合时间=路程÷速度,得出两者相遇的时间,从而判断④不成立;由行驶过程中的路程变化可得出甲、乙两船可以相互望见时,x的取值范围,从而能判断出⑤不成立.由上述即可得出结论.
详解:甲船的速度为20÷0.5=40km/h,
乙船的速度为100÷4=25km/h,①成立;
从A港到C港全程为20+100=120km,②成立;
甲船到达C港的时间为120÷40=3(小时),
43=1小时,③不成立;
设两船相遇的时间为t小时,则有40t25t=20,
解得:![]()
即P点坐标为![]() ④不成立;
④不成立;
甲、乙两船第一次相距10km的时间为(2010)÷(4025)=![]() (小时),
(小时),
甲、乙两船第二次相距10km的时间为(20+10)÷(4025)=2(小时),
甲、乙两船第三次相距10km的时间为(10010)÷25=![]() (小时),
(小时),
即甲、乙两船可以相互望见时,x的取值范围是![]() 和
和![]() ,⑤不成立.
,⑤不成立.
故答案为:①②.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b表示的点在数轴上的位置如图所示:
(1)在数轴上表示出-a、-b的位置;
(2)用“<”表示a、b、-a、-b的大小关系;
(3)若数b与其相反数相距20个单位长度,则b表示的数是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察标志,从图案看既是轴对称图形又是中心对称图形的有( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的分式方程
 无解,则m的值为( )
无解,则m的值为( )
A.﹣1.5
B.1
C.﹣1.5或2
D.﹣0.5或﹣1.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB,△COD是等腰直角三角形,点D在AB上,
(1)求证:△AOC≌△BOD;
(2)若AD=3,BD=1,求CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=
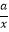 在同一平面直角坐标系中的图象大致是( )
在同一平面直角坐标系中的图象大致是( )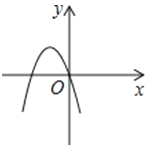
A.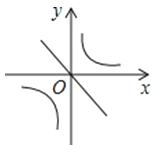
B.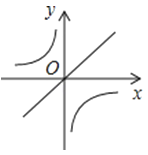
C.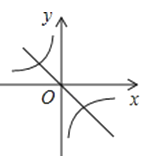
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:

(1)折叠数轴,若1表示的点与-1表示的点重合,则-2表示的点与数 表示的点重合;
(2)折叠数轴,若-1表示的点与5表示的点重合,则4表示的点与 表示的点重合;
(3)已知数轴上点A表示的数是-1,点B表示的数是2,若点A以每秒1个单位长度的速度在数轴上移动,点B以每秒2个单位长度的速度在数轴上移动,且点A始终在点B的左侧,求经过几秒时,A、B两点的距离为6个单位长度.
相关试题

