【题目】如图,将矩形![]() 沿对角线
沿对角线![]() 折叠,点
折叠,点![]() 落到点
落到点![]() 处,
处,![]() 交
交![]() 于点
于点![]()
(1)求证:![]()
(2)若![]() ,求
,求![]() 的值
的值

参考答案:
【答案】(1)见解析 (2)![]()
【解析】
(1)由矩形的性质得到AB∥CD,∠ABD=∠BDC,求得∠BDC=∠DBF,于是得到结论;
(2)根据矩形的性质得到AD=BC,∠A=∠C=90°,根据折叠的性质得到∠A′=∠A=90°,A′D=AD,根据全等三角形的性质得到AF=CF,设AF=CF=x,A′D=BC=2x,根据勾股定理得到![]() ,于是得到结论.
,于是得到结论.
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]()
![]()
又![]()
![]()
![]()
![]() ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴AD=BC,∠A=∠C=90°,
∵将矩形ABCD沿对角线BD折叠,
∴∠A′=∠A=90°,A′D=AD,
∴A′D=BC,∠A′=∠C=90°,
∵∠A′FD=∠BFC,
∴△DA′F≌△BCF(AAS),
![]()
![]()
设![]()
由勾股定理求得![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
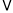
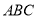 中任一点
中任一点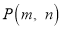 经过平移后对应点为
经过平移后对应点为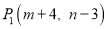 .将
.将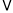
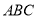 作同样的平移得到
作同样的平移得到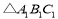 ,已知
,已知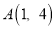 ,
,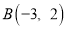 ,
,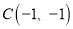 ,
,(1) 在图中画出
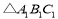 ,;
,;(2) 直接写出
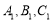 的坐标分别为
的坐标分别为
(3)
 ,的面积为____________.
,的面积为____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图四边形ABCD是菱形,且∠ABC=60,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则下列五个结论中正确的是( )
①若菱形ABCD的边长为1,则AM+CM的最小值1;
②△AMB≌△ENB;
③S四边形AMBE=S四边形ADCM;
④连接AN,则AN⊥BE;
⑤当AM+BM+CM的最小值为2
 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.
A. ①②③ B. ②④⑤ C. ①②⑤ D. ②③⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数a,我们规定:用符号
 表示不大于
表示不大于 的最大整数,称
的最大整数,称 为a的根整数,例如:
为a的根整数,例如: ,
, =3.
=3.(1)仿照以上方法计算:
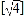 =______;
=______; =_____.
=_____.(2)若
 ,写出满足题意的x的整数值______.
,写出满足题意的x的整数值______.如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次


 =1,这时候结果为1.
=1,这时候结果为1.(3)对100连续求根整数,____次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,已知A(a,0),B(b,3),C(4,0),且满足(a+b)2+|a﹣b+6|=0,线段AB交y轴于F点.
(1)求点A、B的坐标;
(2)点D为y轴正半轴上一点,若ED∥AB,且AM,DM分别平分∠CAB,∠ODE,如图 2,求∠AMD的度数;
(3)如图 3,(也可以利用图 1)①求点F的坐标;②坐标轴上是否存在点P,使得△ABP和△ABC的面积相等?若存在,求出P点坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】乐乐和科学小组的同学们在网上获取了声音在空气中传播的速度与空气温度之间关系的一些数据(如下表)
温度/

-20
-10
0
10
20
30
声速/(
 )
)318
324
330
336
342
348
下列说法中错误的是( )
A.在这个变化过程中,当温度为10
 时,声速是336
时,声速是336
B.温度越高,声速越快
C.当空气温度为20
 时,声音5
时,声音5 可以传播1740
可以传播1740
D.当温度每升高10
 ,声速增加6
,声速增加6
相关试题

