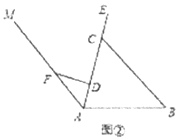
【题目】“4000辆自行车、187个服务网点”,某市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便。图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A,D,C,E在同一条直线上,CD=30 cm,DF=20 cm,AF=25 cm,FD⊥AE于点D,座杆CE=15 cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

参考答案:
【答案】(1)15cm;(2)点E到AB的距离为58.2cm
【解析】分析:(1)根据勾股定理求出AD的长;
(2)作EH⊥AB于H,求出AE的长,根据正弦的概念求出点E到车架AB的距离.
详解:(1)在Rt△ADF中,由勾股定理得,
AD=![]() (cm).
(cm).
(2)AE=AD+CD+EC=15+30+15=60(cm).
过点E作EH⊥AB于H,

在Rt△AEH中,sin∠EAH=![]() ,
,
∴EH=AEsin∠EAH=ABsin75°≈60×0.97=58.2(cm).
答:点E到AB的距离为58.2cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)图①表内的各横行中,从第二个数起的数都比它左边相邻的数大m;各竖列中, 从第二个数起的数都比它上边相邻的数大n.请你仔细观察表格,耐心寻找规律, 根据你得到的规律填空:
①m =______;②n =______;③x =______;④y =______;
(2)若(1)题中的规律不变,把表①中的-1,8和y都去掉,如图②,则x=_______(用含m,n的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( )
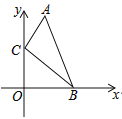
A. (0,0); B. (0,1); C. (0,2); D. (0,3).
-
科目: 来源: 题型:
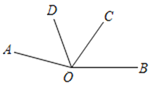
查看答案和解析>>【题目】如图,∠AOB=165°,OD平分∠AOC.
(1)若∠AOD=50°,求∠BOC度数;
(2)若∠BOD=110°,那么OC是∠BOD的平分线吗?说明理由.
-
科目: 来源: 题型:
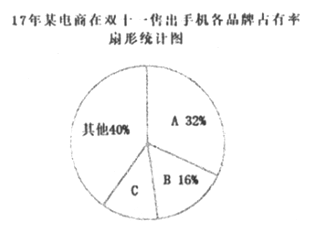
查看答案和解析>>【题目】近几年,移动电商发展迅速,以下是2017年某调查机构发布的相关的统计表和统计图的一部分。请根据以上信息解答下列问题:

(1)2017年10月“移动电商行业用户规模”是___________亿台(结果精确到0.1亿台);并补全条形统计图;
(2)2017年10—12这三个月“移动电商行业用户规模”比上个月增长台数的平均数为___________亿台,若按此平均数增长,请你估计2018年1月“移动电商行业用户规模”为___________亿台(结果精确到0.1亿台);
(3)2017年某电商在双十一共售出手机12000台,则C品牌手机售出的台数是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中假命题有
①相邻的两个角都互补的四边形是平行四边形;②一组对边平行一组对角相等的四边形是平行四边形;③一组对边平行另一组对边相等的四边形是平行四边形;④有一条对角线平分一组对角的四边形是菱形;⑤对角线相等且互相垂直的四边形是正方形.
A. 1个B. 2个
C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与理解:
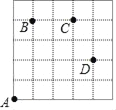
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右) 爬行记为“+”,向下(或向左) 爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中A→C( , ),B→C( , ),D→A( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程.
相关试题

