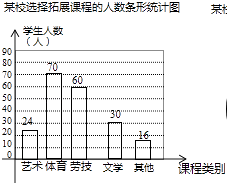
【题目】为深化义务教育课程改革,某校积极开展拓展性课程建设,计划开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程.为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出): 
根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数.
(2)将条形统计图补充完整.
(3)若该校共有1600名学生,请估计全校选择体育类的学生人数.
参考答案:
【答案】
(1)解:60÷30%=200(人),
即本次被调查的学生有200人
(2)解:选择文学的学生有:200×15%=30(人),
选择体育的学生有:200﹣24﹣60﹣30﹣16=70(人),
补全的条形统计图如下图所示,
(3)解:1600× ![]() (人)
(人)
即全校选择体育类的学生有560人.
【解析】(1)根据条形统计图和扇形统计图可知选择劳技的学生60人,占总体的30%,从而可以求得调查学生人数;(2)根据文学的百分比和(1)中求得的学生调查数可以求得文学的有多少人,从而可以求得体育的多少人,进而可以将条形统计图补充完整;(3)根据调查的选择体育的学生所占的百分比可以估算出全校选择体育类的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最大内角等于______

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算。
(1)计算: +(﹣3)2﹣(
+(﹣3)2﹣(  ﹣1)0 .
﹣1)0 .
(2)化简:(2+m)(2﹣m)+m(m﹣1). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中有一个四边形ABCD.
(1)分别写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积;
(3)将四边形ABCD先向下平移3个单位长度,再向右平移4个单位长度后得到的四边形A1B1C1D1,画出四边形A1B1C1D1

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)
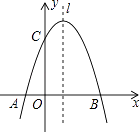
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.

(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC= ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
相关试题

