【题目】⊙O的半径为1,弦AB=![]() ,弦AC=
,弦AC=![]() ,则∠BAC度数为 .
,则∠BAC度数为 .
参考答案:
【答案】75°或15°.
【解析】
试题分析:有两种情况:
①如图1所示:连接OA,过O作OE⊥AB于E,OF⊥AC于F,∴∠OEA=∠OFA=90°,由垂径定理得:AE=BE=![]() ,AF=CF=
,AF=CF=![]() ,cos∠OAE=
,cos∠OAE=![]() =
=![]() ,cos∠OAF=
,cos∠OAF=![]() =
=![]() ,∴∠OAE=30°,∠OAF=45°,∴∠BAC=30°+45°=75°;
,∴∠OAE=30°,∠OAF=45°,∴∠BAC=30°+45°=75°;
②如图2所示:
连接OA,过O作OE⊥AB于E,OF⊥AC于F,∴∠OEA=∠OFA=90°,由垂径定理得:AE=BE=![]() ,AF=CF=
,AF=CF=![]() ,cos∠OAE═
,cos∠OAE═![]() =
=![]() ,cos∠OAF=
,cos∠OAF=![]() =
=![]() ,∴∠OAE=30°,∠OAF=45°,∴∠BAC=45°﹣30°=15°;
,∴∠OAE=30°,∠OAF=45°,∴∠BAC=45°﹣30°=15°;
故答案为:75°或15°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)如果∠OBC=45°,∠OCB=30°,OC=4,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④
 .其中一定成立的是( )
.其中一定成立的是( )A.①②③ B.②③④ C.①③④ D.①②④

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某市八年级学生的肺活量,从中抽样调查了500名学生的肺活量,这项调查中的样本是_______,样本容量是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应推进中小学生素质教育的号召,某校决定在下午15点至16点开设以下选修课:音乐史、管乐、篮球、健美操、油画.为了解同学们的选课情况,某班数学兴趣小组从全校三个年级中各调查一个班级,根据相关数据,绘制如下统计图.

(1)请根据以上信息,直接补全条形统计图(图1)和扇形统计图(图2);
(2)若初一年级有180人,请估算初一年级中有多少学生选修音乐史?
(3)若该校共有学生540人,请估算全校有多少学生选修篮球课?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠B=∠C,求证:∠1=∠2.
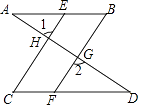
证明:∵AB∥CD(已知)
∴∠B=().
∵∠B=∠C(已知)
∴∠BFD=∠C()
∴∥()
∴∠2=(两直线平行,同位角相等)
∵∠1=()
∴∠1=∠2(等量代换). -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并把不等式①和②的解集在同一数轴上表示出来.
,并把不等式①和②的解集在同一数轴上表示出来.
相关试题

