【题目】如图,已知抛物线y=x2+bx+c与y轴交于点C,与![]() 轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;
轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;
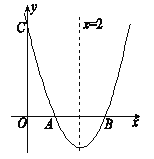
(1) 求抛物线的函数表达式;
(2) 如果抛物线的对称轴上存在一点P,使得△APC周长的最小,求此时△APC周长.
(3) 设D为抛物线上一点,E为对称轴上一点,若以点A、B、D、E为顶点的四边形是菱形,求点D的坐标.(直接写出结果)
参考答案:
【答案】(1) y=x2-4x+3;(2) ![]() .(3) D的坐标为:(2,-1).
.(3) D的坐标为:(2,-1).
【解析】
试题分析:(1)根据抛物线对称轴的定义易求A(1,0),B(3,0).所以1、3是关于x的一元二次方程x2+bx+c=0的两根.由韦达定理易求b、c的值;
(2)如图,连接AC、BC,BC交对称轴于点P,连接PA.根据抛物线的对称性质得到PA=PB,则△APC的周长的最小值=AC+AP+PC=AC+BC,所以根据两点间的距离公式来求该三角形的周长的最小值即可;
(3)如图2,点D是抛物线的顶点,所以根据抛物线解析式利用顶点坐标公式即可求得点D的坐标.
试题解析:(1)∵AB=2,对称轴为直线x=2.
∴点A的坐标是(1,0),点B的坐标是(3,0).
∵抛物线y=x2+bx+c与x轴交于点A,B,
∴1、3是关于x的一元二次方程x2+bx+c=0的两根.
由韦达定理,得
1+3=-b,1×3=c,
∴b=-4,c=3,
∴抛物线的函数表达式为y=x2-4x+3;
(2)连接AC、BC,BC交对称轴于点P,连接PA.
由(1)知抛物线的函数表达式为y=x2-4x+3,A(1,0),B(3,0),
∴C(0,3),
∴BC=![]() ,AC=
,AC=![]() .
.
∵点A、B关于对称轴x=2对称,
∴PA=PB,
∴PA+PC=PB+PC.
此时,PB+PC=BC.
∴点P在对称轴上运动时,(PA+PC)的最小值等于BC.
∴△APC的周长的最小值=AC+AP+PC=AC+BC=![]() .
.
(3)如图2,根据“菱形ADBE的对角线互相垂直平分,抛物线的对称性”得到点D是抛物线y=x2-4x+3的顶点坐标,即(2,-1),
当E、D点在x轴的上方,即DE∥AB,AE=AB=BD=DE=2,此时不合题意,
故点D的坐标为:(2,-1).
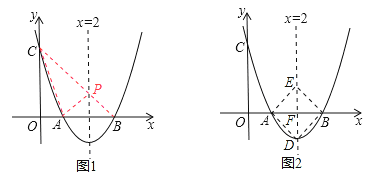
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正多边形的内角和等于外角和2倍,则这个正多边形是( )
A.正方形
B.正五边形
C.正六边形
D.正八边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据:0,1,2,3,3,5,5,10的中位数是( ).
A. 2.5 B. 3 C. 3.5 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知a-b=1,ab=-2,求(a+1)(b-1)的值;
(2)已知
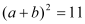 ,
,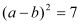 ,求ab;
,求ab;(3)已知x-y=2,y-z=2,x+z=4,求
 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:2x2﹣8= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】由下表估算一元二次方程x2+12x=15的一个根的范围,其中正确的是( )
X
1.0
1.1
1.2
1.3
X2+12x
13
14.41
15.84
17.29
A.1.0<x<1.1
B.1.1<x<1.2
C.1.2<x<1.3
D.14.41<x<15.84
相关试题

