搜索
【题目】由于只有1张市运动会开幕式的门票，小王和小张都想去，两人商量采取转转盘（如图，转盘盘面被分为面积相等，且标有数字1，2，3，4的4个扇形区域）的游戏方式决定谁胜谁去观看．规则如下：两人各转动转盘一次，当转盘指针停止，如两次指针对应盘面数字都是奇数，则小王胜；如两次指针对应盘面数字都是偶数，则小张胜；如两次指针对应盘面数字是一奇一偶，视为平局．若为平局，继续上述游戏，直至分出胜负．
如果小王和小张按上述规则各转动转盘一次，则
（1）小王转动转盘，当转盘指针停止，对应盘面数字为奇数的概率是多少？
（2）该游戏是否公平？请用列表或画树状图的方法说明理由．
参考答案：
【答案】
【解析】
试题分析：（1）根据概率公式直接计算即可；（2）列表得出所有等可能的情况数，找出两指针所指数字都是偶数或都是奇数的概率即可得知该游戏是否公平．
试题解析：（1）∵转盘的4个等分区域内只有1，3两个奇数，
∴小王转动转盘，当转盘指针停止，对应盘面数字为奇数的概率=
；
（2）列表如下：
1 | 2 | 3 | 4 | |
1 | （1，1） | （1，2） | （1，3） | （1，4） |
2 | （2，1） | （2，2） | （2，3） | （2，4） |
3 | （3，1） | （3，2） | （3，3） | （3，4） |
4 | （4，1） | （4，2） | （4，3） | （4，4） |
所有等可能的情况有16种，其中两指针所指数字数字都是偶数或都是奇数的都是4种，
∴P（向往胜）=
，P（小张胜）=
，∴游戏公平．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）
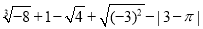
（2）（﹣
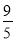a6x5y4）÷（﹣3a2xy2）×（﹣
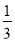ax）2（3）[（x﹣2y）2+（x﹣2y）（x+2y）﹣2x（2x﹣y）]÷2x
-
科目： 来源： 题型：
查看答案和解析>>【题目】四边形ABCD中，∠ABC+∠D＝180°，AC平分∠BAD，CE⊥AB于E，CF⊥AD于F．
（1）求证：△CBE≌△CDF；
（2）若AB＝3，DF＝2，求AF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若 x 满足 (9x)(x4)=4， 求 (4x)2+(x9)2 的值.
设 9x=a，x4=b， 则 (9x)(x4)=ab=4，a+b=(9x)+(x4)=5 ，
∴(9x)2+(x4)2=a2+b2=(a+b)22ab=522×4=13
请仿照上面的方法求解下面问题：
(1)若 x 满足 (5x)(x2)=2， 求 (5x)2+(x2)2 的值
(2)已知正方形 ABCD 的边长为 x ， E ， F 分别是 AD 、 DC 上的点，且 AE=1 ， CF=3 ，长方形 EMFD 的面积是 48 ，分别以 MF 、 DF 作正方形，求阴影部分的面积.
-
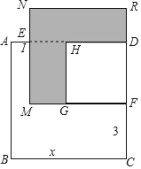
科目： 来源： 题型：
查看答案和解析>>【题目】由于只有1张市运动会开幕式的门票，小王和小张都想去，两人商量采取转转盘（如图，转盘盘面被分为面积相等，且标有数字1，2，3，4的4个扇形区域）的游戏方式决定谁胜谁去观看．规则如下：两人各转动转盘一次，当转盘指针停止，如两次指针对应盘面数字都是奇数，则小王胜；如两次指针对应盘面数字都是偶数，则小张胜；如两次指针对应盘面数字是一奇一偶，视为平局．若为平局，继续上述游戏，直至分出胜负．
如果小王和小张按上述规则各转动转盘一次，则
（1）小王转动转盘，当转盘指针停止，对应盘面数字为奇数的概率是多少？
（2）该游戏是否公平？请用列表或画树状图的方法说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小孟同学将等腰直角三角板ABC（AC＝BC）的直角顶点C放在一直线m上，将三角板绕C点旋转，分别过A，B两点向这条直线作垂线AD，BE，垂足为D，E．
（1）如图1，当点A，B都在直线m上方时，猜想AD，BE，DE的数量关系是 ；
（2）将三角板ABC绕C点按逆时针方向旋转至图2的位置时，点A在直线m上方，点B在直线m下方．（1）中的结论成立吗？请你写出AD，BE，DE的数量关系，并证明你的结论．
（3）将三角板ABC继续绕C点逆时针旋转，当点A在直线m的下方，点B在直线m的上方时，请你画出示意图，按题意标好字母，直接写出AD，BE，DE的数量关系结论 ．
-
科目： 来源： 题型：
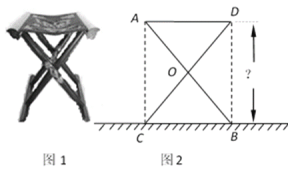
查看答案和解析>>【题目】某大学计划为新生配备如图1所示的折叠椅．图2中的正方形ACBD是折叠椅撑开后的侧面示意图，其中椅腿AB和CD的长相等，O是它们的中点．若正方形ACBD的面积为[9(2x－3y)2+12(2x－3y) (x+4y) +4(x+4y)2]（米2）（x＞y），你能求出这种折叠椅张开后的高度吗？
相关试题
