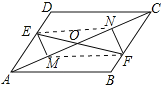
【题目】如图,已知E、F分别为平行四边形ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,求证:

(1)EM=FN;
(2)EF与MN互相平分.
参考答案:
【答案】(1)(2)证明见解析
【解析】
试题分析:(1)由平行四边形的性质得出AD∥BC,AD=BC,得出∠EAM=∠FCN,AE=CF,由AAS证明△AEM≌△CFN,得出对应边相等即可;
(2)连接EN、FM,求出EM=FN,EM∥FN,得出平行四边形EMFN,根据平行四边形的性质得出即可.
证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,
∴∠EAM=∠FCN,
∵DE=BF,
∴AE=CF,∵EM⊥AC于M,FN⊥AC于N,∴∠AME=∠CNF=90°,
在△AEM和△CFN中,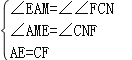 ,
,
∴△AEM≌△CFN(AAS),
∴EM=FN;
(2)连接EN、FM,如图所示:
∵EM⊥AC,FN⊥AC,
∴∠AME=∠EMN=∠FNC=∠FNM=90°,
∴EM∥FN,
又∵由(1)得EM=FN,
∴四边形EMFN是平行四边形,
∴EF与MN互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小知识:如图,我们称两臂长度相等(即
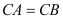 )的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角
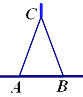
)的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时,若张角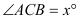 ,则底角
,则底角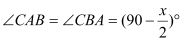 .
.
请运用上述知识解决问题:
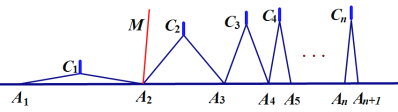
如图,
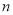 个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下:
个相同规格的等臂圆规的两脚依次摆放在同一条直线上,其张角度数变化如下: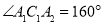 ,
,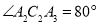 ,
, 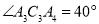 ,
,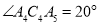 ,…
,…
(1)、①由题意可得
 = ;
= ;②若
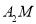 平分
平分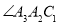 ,则
,则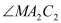 = ;
= ;(2)、
 = (用含
= (用含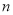 的代数式表示);
的代数式表示);(3)、当
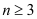 时,设
时,设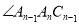 的度数为
的度数为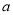 ,
,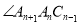 的角平分线
的角平分线 与
与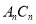 构成的角的度数为
构成的角的度数为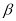 ,那么
,那么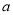 与
与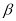 之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)
之间的等量关系是 ,请说明理由. (提示:可以借助下面的局部示意图)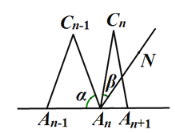
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋中装着3个红球和2个黄球,它们只有颜色上的区别,随机从袋中摸出1个小球,记下颜色不放回,再从袋子中任意取出1个小球,记下颜色:
(1)若取出的第一个小球为红色,则取出的第二个小球仍为红球的概率是 ;
(2)按要求从袋子中取出的两个球,请画出树状图或列表格,并求出取出的两个小球中有1个黄球、1个红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:在用尺规作线段
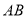 等于线段
等于线段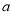 时,小明的具体做法如下:
时,小明的具体做法如下:已知:如图,线段
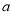 .
. 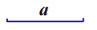
求作:线段
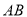 ,使得线段
,使得线段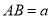 .
.作法: ① 作射线
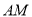 ;② 在射线
;② 在射线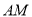 上截取
上截取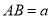 .∴线段
.∴线段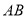 为所求.
为所求.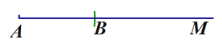
解决下列问题:
已知:如图,线段
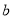 .
. 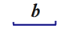
(1)、请你仿照小明的作法,在上图中的射线
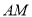 上作线段
上作线段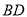 ,使得
,使得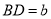 ;(不要求写作法和结论,保留作图痕迹)
;(不要求写作法和结论,保留作图痕迹) (2)、在(1)的条件下,取
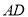 的中点
的中点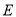 .若
.若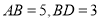 ,求线段
,求线段 的长.(要求:第(2)问重新画图解答)
的长.(要求:第(2)问重新画图解答) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.
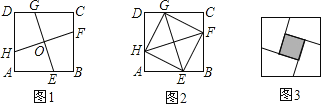
(1)如图2,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;
(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD的边长为3cm,HA=EB=FC=GD=1cm,则图3中阴影部分的面积为 cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 魔术师为大家表演魔术. 他请观众想一个数,然后将这个数按以下步骤操作:

魔术师立刻说出观众想的那个数.
(1)、如果小明想的数是-1,那么他告诉魔术师的结果应该是 ;
(3)、如果小聪想了一个数并告诉魔术师结果为93,那么魔术师立刻说出小聪想的那个数是 ;
(3)、观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数,请你说出其中的奥妙.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果多边形的内角和是外角和的k倍,那么这个多边形的边数是( ).
A.k B.2k+1 C.2k+2 D.2k-2
相关试题

