搜索
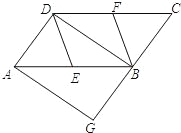
【题目】如图，在ABCD中，E、F分别为边AB、CD的中点，BD是对角线，过点A作AG∥DB，交CB的延长线于点G，∠G=90°．
求证：四边形DEBF是菱形．
参考答案：
【答案】证明参见解析.
【解析】
试题分析：根据已知条件证明BE=DF，BE∥DF，从而得出四边形DFBE是平行四边形，再证明DE=BE，根据邻边相等的平行四边形是菱形，从而得出结论．
试题解析：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．∵点E、F分别是AB、CD的中点，∴BE=
AB，DF=CD．∴BE=DF，BE∥DF，∴四边形DFBE是平行四边形，∵∠G=90°，AG∥BD，AD∥BG，∴四边形AGBD是矩形，∴∠ADB=90°，在Rt△ADB中，∵E为AB的中点，∴AE=BE=DE，∴四边形DEBF是菱形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】分解因式：2x3﹣8x＝_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个不透明的口袋里装有分别标有汉字“幸”、“福”、“聊”、“城”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．
（1）若从中任取一个球，球上的汉字刚好是“福”的概率为多少？
（2）小颖从中任取一球，记下汉字后放回袋中，然后再从中任取一球，求小颖取出的两个球上汉字恰能组成“幸福”或“聊城”的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】直线MN与直线PQ垂直相交于O，点A在直线PQ上运动，点B在直线MN上运动．
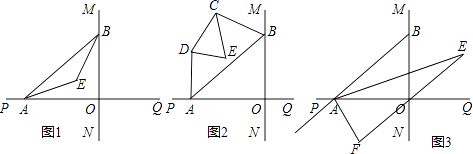
（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A，B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．
（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A，B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．
（3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E，F，在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】数轴上点A到原点的距离为2.5，则点A所表示的数是（ ）.
A.2.5
B.-2.5
C.2.5或-2.5
D.0 -
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC与△DEF相似，其面积比为1：4，则它们的相似比为__________.
-
科目： 来源： 题型：
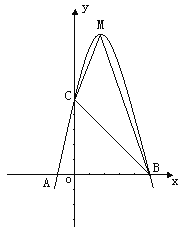
查看答案和解析>>【题目】已知：二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为(-1，0)，点C(0，5)，另抛物线经过点(1，8)，M为它的顶点.
（1)求抛物线的解析式；
(2)求△MCB的面积S△MCB.
相关试题
