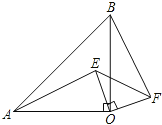
【题目】如图,直角坐标系![]() 中,一次函数
中,一次函数![]() 的图像
的图像![]() 分别与
分别与![]() 、
、![]() 轴交于
轴交于![]() 两点,正比例函数的图像
两点,正比例函数的图像![]() 与
与![]() 交于点
交于点![]() .
.

(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)在坐标轴上找一点![]() ,使以
,使以![]() 为腰的
为腰的![]() 为等腰三角形,请直接写出点
为等腰三角形,请直接写出点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)m=4,l2的解析式为![]() ;(2)5;(3)点P的坐标为(
;(2)5;(3)点P的坐标为(![]() ),(0,
),(0,![]() ),(0,5),(5,0),(8,0),(0,6).
),(0,5),(5,0),(8,0),(0,6).
【解析】
(1)先求得点C的坐标,再运用待定系数法即可得到l2的解析式;
(2)过C作CD⊥AO于D,CE⊥BO于E,则CD=3,CE=4,再根据A(10,0),B(0,5),可得AO=10,BO=5,进而得出S△AOC-S△BOC的值;
(3)由等腰三角形的定义,可对点P进行分类讨论,分别求出点P的坐标即可.
解:(1)把C(m,3)代入一次函数![]() ,可得
,可得
![]() ,
,
解得m=4,
∴C(4,3),
设l2的解析式为y=ax,则3=4a,
解得:a=![]() ,
,
∴l2的解析式为:![]() ;
;
(2)如图,过C作CD⊥AO于D,CE⊥BO于E,则CD=3,CE=4,

由![]() ,令x=0,则y=5;令y=0,则x=10,
,令x=0,则y=5;令y=0,则x=10,
∴A(10,0),B(0,5),
∴AO=10,BO=5,
∴S△AOC-S△BOC=![]() ×10×3
×10×3![]() ×5×4=15-10=5;
×5×4=15-10=5;
(3)∵![]() 是以
是以![]() 为腰的等腰三角形,
为腰的等腰三角形,
则点P的位置有6种情况,如图:

∵点C的坐标为:(4,3),
∴![]() ,
,
∴![]() ,
,
∴点P的坐标为:(![]() ),(0,
),(0,![]() ),(0,5),(5,0),(8,0),(0,6).
),(0,5),(5,0),(8,0),(0,6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级全体同学参加了爱心捐款活动,该校随机抽查了部分同学捐款的情况统计如图:
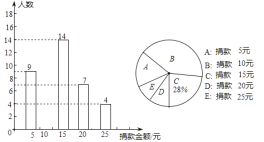
(1)求出本次抽查的学生人数,并将条形统计图补充完整;
(2)捐款金额的众数是___________元,中位数是_____________;
(3)请估计全校八年级1000名学生,捐款20元的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2)、B(0,4)、C(0,2),
(1)画出△ABC关于点C成中心对称的△A1B1C;
(2)平移△ABC:若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(3)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
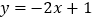 的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数
的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数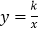 (k≠0)图象在第二象限内的交点.
(k≠0)图象在第二象限内的交点.(1)求点B的坐标及k的值;
(2)试在x轴上确定点C,使AC=AB,请直接写出点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH,添的钢管长度都与OE相等,则最多能添加这样的钢管_____根.
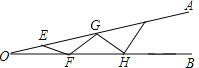
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,等腰Rt△OAB中,∠AOB=90o,等腰Rt△EOF中,∠EOF=90o,连结AE、BF.则AE与BF是什么关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中踏集团销售某种商品,每件进价为10元。在销售过程中发现,平均每天的销售量y(件)与销售价x(元/件)(不低于进价)之间的关系可近似的看做一次函数:
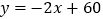 ;
;(1)求中踏集团平均每天销售这种商品的利润w(元)与销售价x之间的函数关系式;
(2)当这种商品的销售价为多少元时,可以获得最大利润,最大利润是多少?
相关试题

