搜索
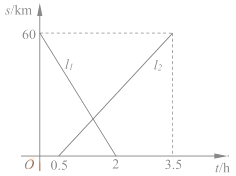
【题目】A、B两地相距60km，甲、乙两人从两地出发相向而行，甲先出发．图中
表示两人离A地的距离S（km）与时间t（h）的关系，结合图像回答下列问题：
（1）表示乙离开A地的距离与时间关系的图像是________(填
）；
甲的速度是__________km/h；乙的速度是________km/h。
（2）甲出发后多少时间两人恰好相距5km？
参考答案：
【答案】
【解析】
试题分析：（1）乙离开A地的距离越来越远，图像是
； 甲的速度60÷2=30；乙的速度60÷（3.5-0.5）=20；
（2）分类讨论：①相遇前：
得
；②相遇后：由
得
.
试题解析：（1）； 30； 20；
（2）由图可求出
，
由得；由得
答：甲出发后1.3h或者1.5h时，甲乙相距5km。
-
科目： 来源： 题型：
查看答案和解析>>【题目】为推动阳光体育活动的广泛开展，引导学生积极参加体育锻炼，学校准备购买一批运动鞋供学生借用．现从各年级随机抽取了部分学生的鞋号，绘制了如下的统计图①和图②，请根据图中提供的信息，解答下列问题：
（1）本次接受随机抽样调查的学生人数为 人，图①中的m的值为 ，图①中“38号”所在的扇形的圆心角度数为 ；
（2）本次调查获取的样本数据的众数是 ，中位数是 ；
（3）根据样本数据，若学校计划购买200双运动鞋，建议购买36号运动鞋多少双？
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题探究
（1）如图①，已知正方形ABCD的边长为4．点M和N分别是边BC、CD上两点，且BM=CN，连接AM和BN，交于点P．猜想AM与BN的位置关系，并证明你的结论．
（2）如图②，已知正方形ABCD的边长为4．点M和N分别从点B、C同时出发，以相同的速度沿BC、CD方向向终点C和D运动．连接AM和BN，交于点P，求△APB周长的最大值；
问题解决
（3）如图③，AC为边长为2
的菱形ABCD的对角线，∠ABC=60°．点M和N分别从点B、C同时出发，以相同的速度沿BC、CA向终点C和A运动．连接AM和BN，交于点P．求△APB周长的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点.
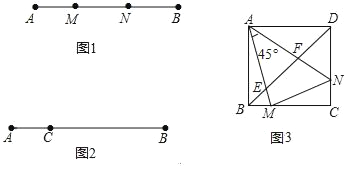
（1）已知点M，N是线段AB的勾股分割点，若AM=3，MN=4求BN的长；
（2）已知点C是线段AB上的一定点，其位置如图2所示，请在BC上画一点D，使C，D是线段AB的勾股分割点（要求尺规作图，保留作图痕迹，画出一种情形即可）；
（3）如图3，正方形ABCD中，M，N分别在BC，DC上，且BM≠DN，∠MAN=45°，AM，AN分别交BD于E，F.
求证：①E、F是线段BD的勾股分割点；
②△AMN的面积是△AEF面积的两倍．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，抛物线 y=
x2﹣
x﹣
与x轴交于A、B、两点（点A在点B的左侧），与y轴交于点C．（1）判断△ABC形状，并说明理由．
（2）在抛物线第四象限上有一点，它关于x轴的对称点记为点P，点M是直线BC上的一动点，当△PBC的面积最大时，求PM+
MC的最小值；（3）如图2，点K为抛物线的顶点，点D在抛物线对称轴上且纵坐标为
，对称轴右侧的抛物线上有一动点E，过点E作EH∥CK，交对称轴于点H，延长HE至点F，使得EF=
，在平面内找一点Q，使得以点F、H、D、Q为顶点的四边形是轴对称图形，且过点Q的对角线所在的直线 是对称轴，请问是否存在这样的点Q，若存在请直接写出点E的横坐标，若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】赛龙舟是端午节的主要习俗，某市甲乙两支龙舟队在端午节期间进行划龙舟比赛，从起点A驶向终点B，在整个行程中，龙舟离开起点的距离y（米）与时间x（分钟）的对应关系如图所示，请结合图象解答下列问题：
（1）起点A与终点B之间相距多远？
（2）哪支龙舟队先出发？哪支龙舟队先到达终点？
（3）分别求甲、乙两支龙舟队的y与x函数关系式；
（4）甲龙舟队出发多长时间时两支龙舟队相距200米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在下列横线上用含有
，
的代数式表示相应图形的面积．（1）①________；②__________；③__________；④_________________．
（2）通过拼图，你发现前三个图形的面积与第四个图形面积之间有什么关系？请用数学式子表示：________________________________________.
（3）利用（2）的结论计算1972+2×197×3+32的值．( 注意不利用以上结论不得分)
相关试题
