【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() 的图象上.
的图象上. 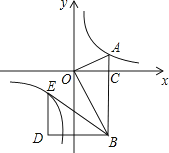
(1)求反比例函数y= ![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP= ![]() S△AOB , 求点P的坐标;
S△AOB , 求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
参考答案:
【答案】
(1)
解:∵点A( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() 的图象上,
的图象上,
∴k= ![]() ×1=
×1= ![]() ,
,
∴反比例函数的表达式为y= ![]()
(2)
解:∵A( ![]() ,1),AB⊥x轴于点C,
,1),AB⊥x轴于点C,
∴OC= ![]() ,AC=1,
,AC=1,
由射影定理得OC2=ACBC,可得BC=3,B( ![]() ,﹣3),
,﹣3),
S△AOB= ![]() ×
× ![]() ×4=2
×4=2 ![]() .
.
∴S△AOP= ![]() S△AOB=
S△AOB= ![]() .
.
设点P的坐标为(m,0),
∴ ![]() ×|m|×1=
×|m|×1= ![]() ,
,
∴|m|=2 ![]() ,
,
∵P是x轴的负半轴上的点,
∴m=﹣2 ![]() ,
,
∴点P的坐标为(﹣2 ![]() ,0)
,0)
(3)
解:点E在该反比例函数的图象上,理由如下:
∵OA⊥OB,OA=2,OB=2 ![]() ,AB=4,
,AB=4,
∴sin∠ABO= ![]() =
= ![]() =
= ![]() ,
,
∴∠ABO=30°,
∵将△BOA绕点B按逆时针方向旋转60°得到△BDE,
∴△BOA≌△BDE,∠OBD=60°,
∴BO=BD=2 ![]() ,OA=DE=2,∠BOA=∠BDE=90°,∠ABD=30°+60°=90°,
,OA=DE=2,∠BOA=∠BDE=90°,∠ABD=30°+60°=90°,
而BD﹣OC= ![]() ,BC﹣DE=1,
,BC﹣DE=1,
∴E(﹣ ![]() ,﹣1),
,﹣1),
∵﹣ ![]() ×(﹣1)=
×(﹣1)= ![]() ,
,
∴点E在该反比例函数的图象上
【解析】本题考查了待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征,三角形的面积,旋转的性质,正确求出解析式是解题的关键.(1)将点A( ![]() ,1)代入y=
,1)代入y= ![]() ,利用待定系数法即可求出反比例函数的表达式;(2)先由射影定理求出BC=3,那么B(
,利用待定系数法即可求出反比例函数的表达式;(2)先由射影定理求出BC=3,那么B( ![]() ,﹣3),计算求出S△AOB=
,﹣3),计算求出S△AOB= ![]() ×
× ![]() ×4=2
×4=2 ![]() .则S△AOP=
.则S△AOP= ![]() S△AOB=
S△AOB= ![]() .设点P的坐标为(m,0),列出方程求解即可;(3)先解△OAB,得出∠ABO=30°,再根据旋转的性质求出E点坐标为(﹣
.设点P的坐标为(m,0),列出方程求解即可;(3)先解△OAB,得出∠ABO=30°,再根据旋转的性质求出E点坐标为(﹣ ![]() ,﹣1),即可求解.
,﹣1),即可求解.
【考点精析】通过灵活运用比例系数k的几何意义,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如右图所示,直线y1=-2x+3和直线y2=mx-1分别交y轴于点A,B,两直线交于点C(1,n).
(1)求m,n的值;
(2)求ΔABC的面积;
(3)请根据图象直接写出:当y1<y2时,自变量的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择.
方案一:每千克种子价格为4元,均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次购买超过3千克,则超出部分的种子打七折.
(1)请分别求出方案一、方案二中购买的种子数量x(千克)与付款金额y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组线段中,可以组成直角三角形的是( )
A. 4,5,6 B. 3,4,5 C. 5,6,7 D. 1,
 ,3
,3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且DE=DC.
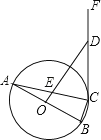
(1)求证:CF是⊙O的切线;
(2)若⊙O的半径为5,BC=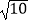 ,求DE的长.
,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC与BD交于O,下列条件中不一定能判定这个四边形是平行四边形的是( )

A. AB=DC,AD=BC B. AD∥BC,AB∥DC
C. OA=OC,OB=OD D. AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.

证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠ (等量代换)
∴EF∥CD( )
∴∠AEF=∠ ( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°( )
∴CD⊥AB( )
相关试题

