【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且DE=DC.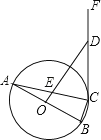
(1)求证:CF是⊙O的切线;
(2)若⊙O的半径为5,BC= ![]() ,求DE的长.
,求DE的长.
参考答案:
【答案】
(1)
证明:连接OC,
∵OA=OC,
∴∠A=∠OCA,
∵OD⊥AB,
∴∠A+∠AEO=90°,
∵DE=DC,
∴∠DEC=∠DCE,
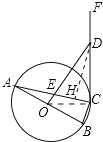
∵∠AEO=∠DCE,
∴∠AEO=∠DCE,
∴∠OCE+∠DCE=90°,
∴∠OCF=90°,
∴OC⊥CF,
∴CF是⊙O切线.
(2)
解:作DH⊥AC于H,则∠EDH=∠A,
∵DE=DC,
∴EH=HC= ![]() EC,
EC,
∵⊙O的半径为5,BC= ![]() ,
,
∴AB=10,AC=3 ![]() ,
,
∵△AEO∽△ABC,
∴ ![]() =
= ![]() ,
,
∴AE= ![]() =
= ![]() ,
,
∴EC=AC﹣AE= ![]() ,
,
∴EH= ![]() EC=
EC= ![]() ,
,
∵∠EDH=∠A,
∴sin∠A=sin∠EDH,
∴ ![]() =
= ![]() ,
,
∴DE= ![]() =
= ![]() =
= ![]()
【解析】(1)连接OC,欲证明CF是⊙O的切线,只要证明∠OCF=90°.
(2)作DH⊥AC于H,由△AEO∽△ABC,得 ![]() =
= ![]() 求出AE,EC,再根据sin∠A=sin∠EDH,得到
求出AE,EC,再根据sin∠A=sin∠EDH,得到 ![]() =
= ![]() ,求出DE即可.本题考查切线的性质、相似三角形的判定和性质、三角函数等知识,解题的关键是添加辅助线,构造相似三角形,属于中考常考题型.
,求出DE即可.本题考查切线的性质、相似三角形的判定和性质、三角函数等知识,解题的关键是添加辅助线,构造相似三角形,属于中考常考题型.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择.
方案一:每千克种子价格为4元,均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次购买超过3千克,则超出部分的种子打七折.
(1)请分别求出方案一、方案二中购买的种子数量x(千克)与付款金额y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组线段中,可以组成直角三角形的是( )
A. 4,5,6 B. 3,4,5 C. 5,6,7 D. 1,
 ,3
,3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(
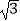 ,1)在反比例函数y=
,1)在反比例函数y= 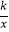 的图象上.
的图象上. 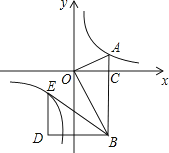
(1)求反比例函数y=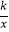 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP= S△AOB , 求点P的坐标;
S△AOB , 求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC与BD交于O,下列条件中不一定能判定这个四边形是平行四边形的是( )

A. AB=DC,AD=BC B. AD∥BC,AB∥DC
C. OA=OC,OB=OD D. AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.

证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠ (等量代换)
∴EF∥CD( )
∴∠AEF=∠ ( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°( )
∴CD⊥AB( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,二次函数y=﹣x2+bx+c的图象过点A(3,0),B(0,4)两点,动点P从A出发,在线段AB上沿A→B的方向以每秒2个单位长度的速度运动,过点P作PD⊥y于点D,交抛物线于点C.设运动时间为t(秒).
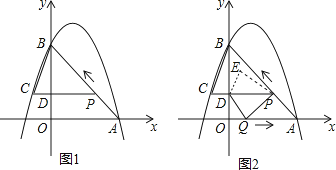
(1)求二次函数y=﹣x2+bx+c的表达式;
(2)连接BC,当t= 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图2,动点P从A出发时,动点Q同时从O出发,在线段OA上沿O→A的方向以1个单位长度的速度运动.当点P与B重合时,P、Q两点同时停止运动,连接DQ,PQ,将△DPQ沿直线PC折叠得到△DPE.在运动过程中,设△DPE和△OAB重合部分的面积为S,直接写出S与t的函数关系及t的取值范围.
相关试题

