【题目】为了更好治理和净化运河,保护环境,运河综合治理指挥部决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格、月处理污水量如下表.经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格(万元/台) | | |
处理污水量(吨/月) | 220 | 180 |
(1)求![]() 的值;
的值;
(2)由于受资金限制,运河综合治理指挥部决定购买污水处理设备的资金既不少于108万元也不超过110万元,问有哪几种购买方案?每月最多能处理污水多少吨?
参考答案:
【答案】(1) a,b的值分别是12和10;(2)有2种方案,分别是购买A型设备4台,B型设备6台或购买A型设备5台,B型设备5台,最多能处理污水2000吨
【解析】
(1)根据购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元,列出方程组,求出方程组的解即可;
(2)设购买A型设备x台,则B型设备(10-x)台,能处理污水y吨,根据购买污水处理设备的资金既不少于108万元也不超过110万元,列出不等式组,求出不等式组的解集,得出购买方案,再根据每月处理污水量的吨数,即可得出答案.
(1)根据题意,得![]() ,
,
解得:![]() .
.
答:a,b的值分别是12和10.
(2)设购买A型设备x台,则B型设备(10-x)台,能处理污水y吨,根据题意得:![]() ,
,
解得:4≤x≤5,
∵x为正整数,
∴有2种购买方案,
方案1:购买A型设备4台,则B型设备6台;
方案2:购买A型设备5台,则B型设备5台;
∵y=220x+180(10-x)=40x+1800,
∴y随x的增大而增大,
当x=5时,y=40×5+1800=2000(吨),
则最多能处理污水2000吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣
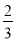 x2
x2【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣
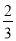 ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣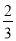 x2.
x2.考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15【题目】在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计解析,绘制了如下不完整的统计表和统计图(图).
次数
10
8
6
5
人数
3
a
2
1
(1)表中a= ;
(2)请将条形统计图补充完整;
(3)从小组成员中任选一人向学校汇报义工活动情况,参加了10次活动的成员被选中的概率有多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】初二年级教师对试卷讲评课中学生参与情况进行调查,调查项目分为主动质疑、独立思考、专注听讲、讲解题目四项.调查组随机抽取了若干名初中学生的参与情况,绘制了如图所示的扇形统计图和条形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为______度;
(2)请将频数分布直方图补充完整;
(3)如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,∠BOC= .
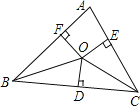
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?

相关试题

