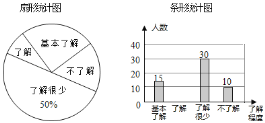
【题目】“校园安全”受到全社会的广泛关注,信丰县某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形圆心角是 度;
(2)请补全条形统计图;
(3)若该中学共有学生1200人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.
参考答案:
【答案】(1)60,90;(2)补图见解析;(3)400人.
【解析】
(1)由了解很少的有30人,占50%,可求得接受问卷调查的学生数,继而求得扇形统计图中“基本了解”部分所对应扇形的圆心角;
(2)由(1)可求得了解的人数,继而补全条形统计图;
(3)利用样本估计总体的方法,即可求得答案.
(1)∵了解很少的有30人,占50%,
∴接受问卷调查的学生共有:30÷50%=60(人);
∴扇形统计图中“基本了解”部分所对应扇形的圆心角为:![]() ×360°=90°;
×360°=90°;
故答案为:60,90;
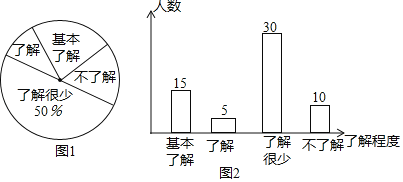
(2)60﹣15﹣30﹣10=5;
补全条形统计图得:
(3)根据题意得:1200×![]() =400(人),
=400(人),
则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为400人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,OD⊥BC于E.
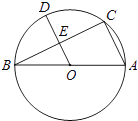
(1)求证:OD∥AC;
(2)若BC=8,DE=3,求⊙O的直径. -
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3,4,5,x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验.实验数据如下表:
摸球总次数
10
20
30
60
90
120
180
240
330
450
“和为8”出现的频数
2
10
13
24
30
37
58
82
110
150
“和为8”出现的频率
0.20
0.50
0.43
0.40
0.33
0.31
0.32
0.34
0.33
0.33
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是;
(2)当x=7时,请用列表法或树状图法计算“和为8”的概率;并判断x=7是否可能. -
科目: 来源: 题型:
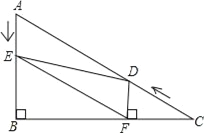
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,BC=5
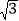 ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.(1)AC的长是 ,AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)当t为何值,△BEF的面积是2
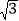 ?
?
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①在直角三角形ABC中,已知两边长为3和4,则第三边长为5;
②三角形的三边a、b、c满足a2+c2=b2,则∠C=90°;
③△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④△ABC中,若 a:b:c=1:2:
 ,则这个三角形是直角三角形.
,则这个三角形是直角三角形.其中,正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架长2.5m的梯子AB斜靠在墙AC上,∠C=90°,此时,梯子的底端B离墙底C的距离BC为0.7m.
(1)求此时梯子的顶端A距地面的高度AC;
(2)如果梯子的顶端A下滑了0.9m,那么梯子的顶端B在水平方向上向右滑动了多远?

-
科目: 来源: 题型:
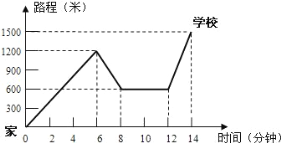
查看答案和解析>>【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
相关试题

