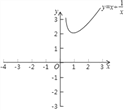
【题目】某数学兴趣小组对函数y=x+![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
x | … | ﹣3 | ﹣2 | ﹣1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | m | ﹣2 | - | - |
|
| 2 |
|
| … |
(1)自变量x的取值范围是 ,m= .
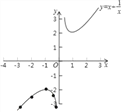
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现:
①方程x+![]() =3有 个实数根;
=3有 个实数根;
②若关于x的方程x+![]() =t有2个实数根,则t的取值范围是 .
=t有2个实数根,则t的取值范围是 .
参考答案:
【答案】(1)x≠0;﹣![]() ;(2)见解析;(3)①函数图象关于原点中心对称;②当x>1时,y的值随x值的增大而增大.(4)①2;②t<﹣2或t>2.
;(2)见解析;(3)①函数图象关于原点中心对称;②当x>1时,y的值随x值的增大而增大.(4)①2;②t<﹣2或t>2.
【解析】试题分析:(1)由分母不能为零,即可得出自变量x的取值范围;
(2)描点、连线,画出函数图象即可;
(3)根据函数的图像,得到写出相应的两条性质即可;
(4)①根据题意知方程的解,即为函数的图像与y=3的交点的个数;
②根据图像的的位置,得到函数有两个交点的t的取值范围.
试题解析:解:(1)∵x在分母上,∴x≠0.
当x=﹣2时,m=y=﹣2+![]() =﹣
=﹣![]() .
.
故答案为:x≠0;﹣![]() .
.
(2)描点、连线,画出函数图象,如图所示.
(3)观察函数图象,可找出函数性质:
①函数图象关于原点中心对称;②当x>1时,y的值随x值的增大而增大.
(4)①方程x+![]() =3可看成函数y=x+
=3可看成函数y=x+![]() 的图象与直线y=3的交点的个数,
的图象与直线y=3的交点的个数,
∵函数y=x+![]() 的图象与直线y=3有两个交点,
的图象与直线y=3有两个交点,
∴方程x+![]() =3有2个实数根.
=3有2个实数根.
故答案为:2.
②观察函数图象可知,当t<﹣2或t>2时,函数y=x+![]() 的图象与直线y=t有两个交点.
的图象与直线y=t有两个交点.
故答案为:t<﹣2或t>2.
-
科目: 来源: 题型:
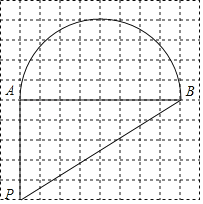
查看答案和解析>>【题目】在每个小正方形的边长为1的网格中,有以AB为直径的半圆和线段AP,AB组成的一个封闭图形,点A,B,P都在网格点上.
(Ⅰ)计算这个图形的面积为_____;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一条能够将这个图形的面积平分的直线,并简要说明这条直线是如何找到的(不要求证明)_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“一带一路”战略的影响下,某茶叶经销商准备把“茶路”融入“丝路”,经计算,他销售10kgA级别和20kgB级别茶叶的利润为4000元,销售20kgA级别和10kgB级别茶叶的利润为3500元.
(1)求每千克A级别茶叶和B级别茶叶的销售利润;
(2)若该经销商一次购进两种级别的茶叶共200kg用于出口,其中B级别茶叶的进货量不超过A级别茶叶的2倍,请你帮该经销商设计一种进货方案使销售总利润最大,并求出总利润的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年10月第二届换广西公路自行车世界巡回赛开赛,有来自世界各地的多支顶级车队参赛,在本次赛事上,组委会把若干翻译志愿者分配给各车队.若毎支车队分配3人,则多出10人,若每支车队分配4人,则还缺8人.
(1)请问一共有几支车队参赛?
(2)组委会给每位参赛车手提供两张号码布和一个电子计时芯片,现有两家供应商提供了如下报价:
①若有
 名选手参赛,请用含
名选手参赛,请用含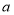 的式子分别表示甲、乙两家供应商所需的费用;
的式子分别表示甲、乙两家供应商所需的费用;②请你通过计算说明组委会会选择哪个供应商比较省钱.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑自行车从A地到B地,乙骑自行车从B地到A地两人都均速前进,已知两人在上午8点同时出发,到上午10时,两人还相距36千米,到中午12时,两人又相距36千米.
(1)列方程,求A、B两地间的路程.
(2)请指出在解答时利用的等量关系是什么?
(3)请你利用其它的等量关系再列出方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察思考:

(1)在∠AOB内部画1条射线OC,则图中有3个不同的角;
(2)在∠AOB内部画2条射线OC、OD,则图中有几个不同的角?
(3)3条射线呢?你能发现什么规律,表示出n条射线能有几个不同的角?
请你先解答以上问题,再结合已学过的知识,针对类似的图形也提出三个问题并作答.(要求:画出图形,写出题干,提出问题并作答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
相关试题

