【题目】观察思考:

(1)在∠AOB内部画1条射线OC,则图中有3个不同的角;
(2)在∠AOB内部画2条射线OC、OD,则图中有几个不同的角?
(3)3条射线呢?你能发现什么规律,表示出n条射线能有几个不同的角?
请你先解答以上问题,再结合已学过的知识,针对类似的图形也提出三个问题并作答.(要求:画出图形,写出题干,提出问题并作答)
参考答案:
【答案】(2)6;(3)10;有![]() 个不同的角;提出三个问题并作答见解析.
个不同的角;提出三个问题并作答见解析.
【解析】
(2)根据图1直接数出即可;
(3)在图1的基础上看增加的角的个数即得画3条射线时角的个数;依此规律可得在∠AOB内部画n条射线时角的个数;把角换成线段,增加的射线条数换成线段上点的个数解答即可.
解:(2)在∠AOB内部画2条射线OC、OD,如图1,则图中有∠AOC、∠AOD、∠AOB、∠COD、∠COB、∠DOB共1+2+3=6个不同的角;
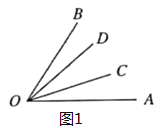
(3)在∠AOB内部画3条射线OC、OD、OE,如图2,在图1 的基础上增加了∠AOE、∠COE、∠DOE和∠BOE,共有6+4=10个不同的角;
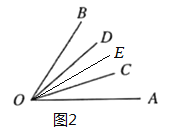
若在∠AOB内部画n条射线,则有![]() 个不同的角.
个不同的角.
提出问题:
(1)如图3,线段AB上有一个点C,则图3中共有 条不同的线段;
(2)如图4,线段AB上有两个点C、D,则图中共有几条不同的线段?
(3)线段AB上有3个点呢?你能发现什么规律,表示出线段AB上有n个点时能有几条不同的线段?
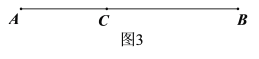

解:(1)图3中有:AC、AB、CB共3条不同的线段;
故答案为:3;
(2)如图4,图中有:AC、AD、AB、CD、CB、DB共1+2+3=6条线段;
(3)线段AB上有3个点C、D、E时,如图5,在图4的基础上增加了线段AE、BE、CE和DE,共有6+4=10条不同的线段;
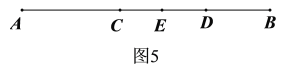
线段AB上有n个点时,则有![]() 条不同的线段.
条不同的线段.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年10月第二届换广西公路自行车世界巡回赛开赛,有来自世界各地的多支顶级车队参赛,在本次赛事上,组委会把若干翻译志愿者分配给各车队.若毎支车队分配3人,则多出10人,若每支车队分配4人,则还缺8人.
(1)请问一共有几支车队参赛?
(2)组委会给每位参赛车手提供两张号码布和一个电子计时芯片,现有两家供应商提供了如下报价:
①若有
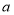 名选手参赛,请用含
名选手参赛,请用含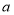 的式子分别表示甲、乙两家供应商所需的费用;
的式子分别表示甲、乙两家供应商所需的费用;②请你通过计算说明组委会会选择哪个供应商比较省钱.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组对函数y=x+
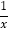 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.x
…
﹣3
﹣2
﹣1
-

-



1
2
3
…
y
…
-
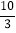
m
﹣2
-

-
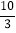
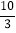

2

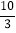
…
(1)自变量x的取值范围是 ,m= .
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现:
①方程x+
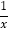 =3有 个实数根;
=3有 个实数根;②若关于x的方程x+
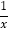 =t有2个实数根,则t的取值范围是 .
=t有2个实数根,则t的取值范围是 .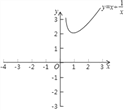
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑自行车从A地到B地,乙骑自行车从B地到A地两人都均速前进,已知两人在上午8点同时出发,到上午10时,两人还相距36千米,到中午12时,两人又相距36千米.
(1)列方程,求A、B两地间的路程.
(2)请指出在解答时利用的等量关系是什么?
(3)请你利用其它的等量关系再列出方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知整数a1,a2,a3,a4,……滿足下列条件:a1=0,a2=-│a1+1│,a3=-│a2+2│,a4=-│a3+3│,·……,依次类推,则a2017的值为 ( )
A.-1007B.-1008C.-1009D.-2016
-
科目: 来源: 题型:
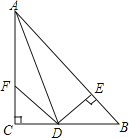
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF,BC=8,AB=10,则△FCD的面积为__________.
相关试题

