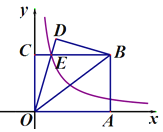
【题目】如图,在直角坐标系中,矩形OABC的顶点A在x轴上,顶点C在y轴上,B(4,3),连接OB,将△OAB沿直线OB翻折,得△ODB,OD与BC相交于点E,若双曲线![]() 经过点E,则k=_____;
经过点E,则k=_____;
参考答案:
【答案】![]()
【解析】由翻折可知BD=OC, ∠D=∠BCO, 又∵∠CEO=∠DEB,
∴△COE∽△DBE.
∴OE=BE,
设CE=x,则OE=8-x,
在Rt△COE中,根据勾股定理得OC+CE=OE,即3+x=(4-x),解得![]() ,
,
∴k=![]() .
.
点睛:折叠与翻折类试题主要有四个特点:(1)折叠与翻折类试题常常与线段垂直平分线,等腰三角形,全等三角形,相似三角形,解直角三角形等内容结合在一起;(2)在折叠与翻折的过程中寻找不变量,在折叠与翻折的过程中挖掘新生成的特殊图形(或常见的基本图形),立足翻折不变量,考查翻折的新生成;(3)将方程,锐角三角函数,解直角三角形和折叠与翻折融合在一起考查;(4)直角,中点,角平分线,相似三角形,锐角三角函数,解直角三角形,方程思想,转化与化归是解决折叠与翻折问题的常见关键词.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E、F分别是BC、CD上的动点(不与点B,C,D重合),且∠EAF=45°,AE、AF与对角线BD分别相交于点G、H,连接EH、EF,则下列结论:
① △ABH∽△GAH; ② △ABG∽△HEG; ③ AE=
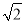 AH; ④ EH⊥AF; ⑤ EF=BE+DF
AH; ④ EH⊥AF; ⑤ EF=BE+DF其中正确的有( )
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
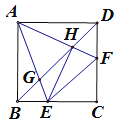
查看答案和解析>>【题目】在如图所示的方格纸中.
(1)作出△ABC关于MN对称的图形△A1B1C1;
(2)说明△A2B2C2是由△A1B1C1经过怎样的平移变换得到的?
(3)若点A在直角坐标系中的坐标为(﹣1,3),试写出A1、B1、C2坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列所给图形中,既是中心对称图形又是轴对称图形的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=2,ab=1,则a2b+ab2的值为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简m﹣n﹣(m+n)的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题情境】:
如图1,AB//CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE//AB,通过平行线性质来求∠APC.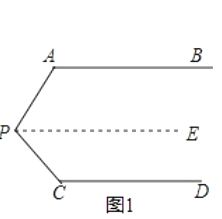
(1)按小明的思路,求∠APC的度数;
(2)【问题迁移】:
如图2,AB//CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)【问题应用】:
在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
相关试题

