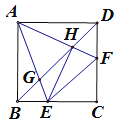
【题目】如图,正方形ABCD中,点E、F分别是BC、CD上的动点(不与点B,C,D重合),且∠EAF=45°,AE、AF与对角线BD分别相交于点G、H,连接EH、EF,则下列结论:
① △ABH∽△GAH; ② △ABG∽△HEG; ③ AE=![]() AH; ④ EH⊥AF; ⑤ EF=BE+DF
AH; ④ EH⊥AF; ⑤ EF=BE+DF
其中正确的有( )
A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】D
【解析】①∵四边形ABCD是正方形,
∴∠ABD=45°,∵∠EAF=45°,
∴∠ABD=∠EAF,
又∵∠AHB=∠AHB,
∴△ABH∽△GAH. ∴①正确;
②∵∠DBC=∠EAF=45°,
∴A,B,E,H四点共圆,
∴∠ABH=∠AEH=45°,
又∵∠BGA=∠EGH,
∴△ABG∽△HEG, ∴②正确;
③∵∠HAE=∠AEH=45°,
∴△AEH为等腰直角三角形,
∴AE=![]() AH,
AH,
∴③正确;
④由③得△AEH为等腰直角三角形,
∴EH⊥AF,
∴④正确;
⑤把△ABE逆时针旋转90得到△ADM,
∴BE=MD,AE=AM,
∵∠EAF=45,
∴∠FAM=9045=45,
∴∠EAF=∠FAM,
在△AEF和△AMF中,
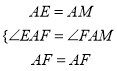
∴△AEF≌△AMF(SAS),
∴EF=MF,
即EF=MD+DF,
∴EF=BE+DF;故⑤正确;
故选D.
点睛:在正方形条件下证明三角形相似,通常利用旋转的性质,等腰三角形的性质,角平分线性质,勾股定理等知识来证明;证明线段之间的数量关系和位置关系一般会利用全等三角形的判定与性质,正方形的性质等来解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,分别以点A和点B为圆心,大于
 AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2=4x-4的解是________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a﹣7b=﹣2,则﹣2a+14b+4的值是( )
A.0
B.2
C.4
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格纸中.
(1)作出△ABC关于MN对称的图形△A1B1C1;
(2)说明△A2B2C2是由△A1B1C1经过怎样的平移变换得到的?
(3)若点A在直角坐标系中的坐标为(﹣1,3),试写出A1、B1、C2坐标.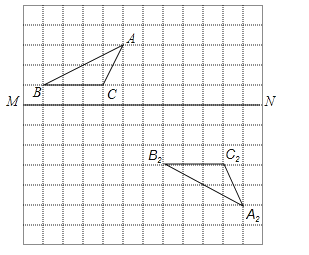
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列所给图形中,既是中心对称图形又是轴对称图形的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,矩形OABC的顶点A在x轴上,顶点C在y轴上,B(4,3),连接OB,将△OAB沿直线OB翻折,得△ODB,OD与BC相交于点E,若双曲线
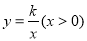 经过点E,则k=_____;
经过点E,则k=_____;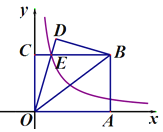
相关试题

