【题目】在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下表是测得的弹簧的长度y与所挂物体的质量x的几组对应值.

(1)上述反映了哪两个变量之问的关系?哪个是自变量?哪个是因变量?
(2)当所挂重物为3kg时,弹簧有多长?不挂重物呢?
(3)若所挂重物为6kg时(在弹簧的允许范围内),你能说出此时弹簧的长度吗?
参考答案:
【答案】(1)上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;(2)当所挂物体重量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米;(3)30厘米
【解析】试题分析: (1)因为表中的数据主要涉及到弹簧的长度和所挂物体的质量,所以反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量;弹簧的长度是因变量;
(2)由表可知,当物体的质量为3kg时,弹簧的长度是24cm;不挂重物时,弹簧的长度是18cm;
(3)由表中的数据可知,x=0时,y=18,并且每增加1千克的质量,长度增加2cm,依此可求所挂重物为6千克时(在允许范围内)时的弹簧长度.
试题解析:
(1)上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;
(2)当所挂物体重量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米;
(3)根据上表可知所挂重物为6千克时(在允许范围内)时的弹簧长度=18+2×6=30厘米.
点睛: 考查了函数的表示方法,本题需仔细分析表中的数据,进而解决问题.明确变量及变量之间的关系是解好本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2+4x+1=0,配方后的方程是( )
A.(x+2)2=5
B.(x﹣2)2=3
C.(x﹣2)2=5
D.(x+2)2=3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个由50个偶数排成的数阵,请你观察框内的四个数之间的关系并解答下列问题:在数阵中任意作一个类似图中的框.
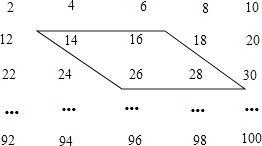
(1)设框内左上角的数为x,那么其他三个数分别是: , ,
(2)如果框内四个数的和是172,这四个数分别是什么?
(3)框内四个数的和有没有可能是322,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
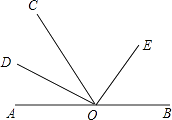
(1)与∠AOE互补的角是 .
(2)若∠AOC=72°,求∠DOE的度数;
(3)当∠AOC=x时,请直接写出∠DOE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于C点,对称轴与抛物线相交于点M,与x轴相交于点N.点P是线段MN上的一动点,过点P作PE⊥CP交x轴于点E.
(1)直接写出抛物线的顶点M的坐标是 .
(2)当点E与点O(原点)重合时,求点P的坐标.
(3)点P从M运动到N的过程中,求动点E的运动的路径长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】乐平街上新开张了一家“好又多”超市,这个星期天,张明和妈妈去这家新开张的超市买东西,如图反映了张明从家到超市的时间t(分钟)与距离s(米)之间关系的一幅图.
(1)图中反映了哪两个变量之间的关系?超市离家多远?
(2)张明从家出发到达超市用了多少时间?从超市返回家花了多少时间?
(3)张明从家出发后20分钟到30分钟内可能在做什么?
(4)张明从家到超市时的平均速度是多少?返回时的平均速度是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】若把一次函数y=2x﹣3,向下平移3个单位长度,得到图象解析式是( )
A. y=2x B. y=2x﹣6 C. y=5x﹣3 D. y=﹣x﹣3
相关试题

