【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整;
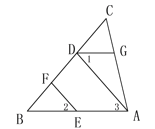
解:∵EF∥AD
∴ =∠3 (两直线平行,同位角相等)
又∵∠1=∠2
∴∠1=∠3 (__________________)
∴ ∥DG (__________________________)
∴∠BAC+______=180°(_________________________)
∵∠BAC=70°
∴∠AGD=_______.
参考答案:
【答案】见解析
【解析】
由EF与AD平行,利用两直线平行,同位角相等得到一对角相等,再由已知角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到AB与DG平行,利用两直线平行同旁内角互补得到两个角互补,即可求出所求角的度数.
∵EF∥AD,
∴∠2=∠3 (两直线平行,同位角相等),
又∵∠1=∠2,
∴∠1=∠3 (等量代换),
∴AB ∥DG (内错角相等,两直线平行),
∴∠BAC+∠AGD =180°(两直线平行,同旁内角互补),
∵∠BAC=70°,
∴∠AGD=110°,
故答案为:∠2;等量代换;AB;内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;110°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 经过点
经过点 ,
, .
.
(1)求直线
 的解析式;
的解析式;(2)若直线
 与直线
与直线 相交于点
相交于点 ,求点
,求点 的坐标;
的坐标;(3)根据图象,直接写出关于
 的不等式
的不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数:
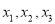 ,称为数列
,称为数列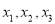 .计算
.计算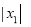 ,
, 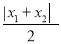 ,
, 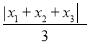 将这三个数的最小值称为数列
将这三个数的最小值称为数列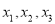 的价值.例如,对于数列2,﹣1,3,因为
的价值.例如,对于数列2,﹣1,3,因为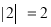 ,
, 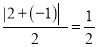 ,
, 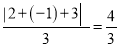 ,所以数列2,﹣1,3的价值为
,所以数列2,﹣1,3的价值为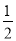 .
.小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列﹣1,2,3的价值为
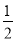 ;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为
;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为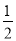 .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:(1)数列﹣4,﹣3,2的价值为 ;
(2)将“﹣4,﹣3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的价值的最小值为 ,取得价值最小值的数列为 (写出一个即可);
(3)将2,﹣9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a的值为 .
-
科目: 来源: 题型:
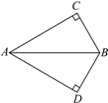
查看答案和解析>>【题目】如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要添加的条件是________或________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有个点
 ,点
,点 第1次向上跳动1个单位至点
第1次向上跳动1个单位至点 ,紧接着第2次向左跳动2个单位至点
,紧接着第2次向左跳动2个单位至点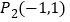 ,第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第200次跳动至点
,第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第200次跳动至点 的坐标是( )
的坐标是( )
A. (51,100)B. (50,100)C. (-50,100)D. (-51,100)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某村为了尽早摆脱贫穷落后的现状,积极响应国家号召,15位村民集资8万元,承包了一些土地种植有机蔬菜和水果,种这两种作物每公顷需要人数和投入资金如下表:

现有条件下,这15位村民应承包多少公顷土地,怎样安排能使得每人都有事可做,并且资金正好够用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知a+b=﹣
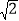 ,求代数式(a﹣1)2+b(2a+b)+2a的值.
,求代数式(a﹣1)2+b(2a+b)+2a的值.(2)已知a,b,c是三角形的三边,且a2+b2+c2﹣ab﹣bc﹣ac=0.求证:此三角形是等边三角形.
相关试题

