【题目】如图,二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.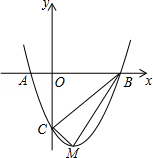
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标,若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵函数y=ax2+bx﹣3的图象经过点A(﹣1,0),B(3,0),
∴ ![]() ,解得:
,解得: ![]()
∴二次函数解析式为y=x2﹣2x﹣3
(2)
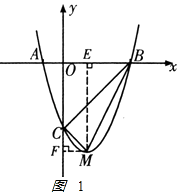
解:△BCM为直角三角形.
如图1
 ,
,
作MF⊥y轴于F,ME⊥x轴于E
∵y=x2﹣2x﹣3=(x﹣1)2﹣4
∴顶点M(1,﹣4).
当x=0时,y=﹣3,
∴C(0,﹣3).
∴在Rt△CMF中,CM2=CF2+MF2=12+12=2,
在Rt△CBO中,CB2=OC2+OB2=32+32=18,
在Rt△EMB中,BM2=ME2+BE2=42+22=20,
∴CM2+CB2=BM2,
∴∠MCB=90°,
∴△BCM为直角三角形
(3)
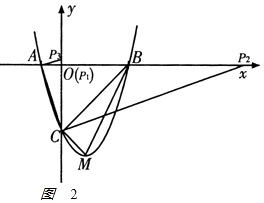
解:如图2
 ,
,
在坐标轴上存在点P,使得以点P,A,C为顶点的三角形与△BCM相似.
如图分三种情形:①若假设点P在x轴上,构成以AC为斜边的Rt△ACP,由△PAC∽△CMB,得
![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴AP=1.
由A(﹣1,0)与点P在x轴上,可知P与原点重合,即点P的坐标为(0,0).
②假设点P在x轴上,构成以AC为直角边的Rt△ACP,由△ACP∽△MCB,
得 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴PA=10,
∴PO=9,
∴P(9,0).
③若假设点P在y轴上,构成以 AC 为直角边的 Rt△ACP,
由△ACP∽△CBM,得
![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴PC= ![]() ,
,
∴PO= ![]() ,
,
∴P(O, ![]() ).
).
综上所述,符合条件的点P的坐标为(0,0),(9,0),(O, ![]() )
)
【解析】(1)根据待定系数法,可得答案;(2)根据勾股定理即勾股定理的逆定里,可得答案;(3)根据相似三角形的性质,可得AP,PC的长,根据点的坐标,可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大家在学完勾股定理的证明后发现运用“同一图形的面积不同表示方式相同”可 以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.学有所用:在等腰 三角形 ABC中,AB=AC,其一腰上的高为h,M 是底边BC上的任意一点,M 到腰AB、AC 的距离分别为 h1、h2 .
(1)请你结合图形来证明: h1+h2=h;
(2)当点M在BC延长线上时,h1、h2、h 之间又有什么样的结论.请你画出图形,并直
接写出结论不必证明;
(3)利用以上结论解答,如图在平面直角坐标系中有两条直线l1:y=x+3,l2:y=-3x+3
若 l2上的一点M 到l1的距离是
 ,求点 M 的坐标.
,求点 M 的坐标.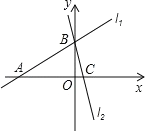
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一张纸对折1次后,就得到2层;对折2次后,就得到4层;对折3次后,就得到8层;……,按照这样对折下去.
(1)求将一张纸对折6次后,层数是多少?
(2)求将一张纸对折n次后,层数是多少(用含n的式子表示)?
(3)若一张纸的厚度均为0.5mm,求将该纸张对折2018次后的总的厚度是多少mm?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,四边形ABCD、CEFG均为正方形.

(1)求证:BE=DG.
(2)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.是否仍存在结论BE=DG,若不存在,请说明理由;若存在,给出证明.
(3)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车间同时开始加工一批零件,从开始加工到加工完这批零件,甲车间工作了9小时,乙车间在中途停工一段时间维修设备,修好后马上按停工前的工作效率继续加工,直到与甲车间同时完成这批零件的加工任务为止,设甲、乙两车间各自加工零件的数量为y(个),甲车间加工的时间为x(时),y与x之间的函数图象如图所示,下列说法其中正确的个数为( )
①这批零件的总个数为1260个;
②甲车间每小时加工零件个数为80个;
③乙车间维修设备后,乙车间加工零件数量y与x之间的函数关系式y=60x﹣120;
④乙车间维修设备用了2个小时
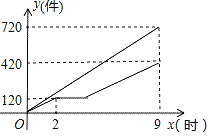
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个菱形两条对角线长的和是10,菱形的面积是12,则菱形的边长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD的对角线AC、BD的长分别为10厘米、6厘米,且AC与BD互相垂直,顺次连接四边形ABCD四边的中点E、F、G、H得四边形EFGH,则四边形EFGH的面积为_____平方厘米.
相关试题

