Question

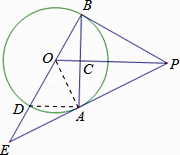
【题目】如图，PA为⊙O的切线，A为切点，过A作OP的垂线AB，垂足为点C，交⊙O于点B，延长BO与⊙O交于点D，与PA的延长线交于点E．
（1）求证：PB为⊙O的切线；
（2）若tan∠ABE= ，求sin∠E．

Answer 1

【答案】
（1）证明：连接OA，

∵PA为⊙O的切线，

∴OA⊥PA

∴∠PAO=90°，

∵OA=OB，OP⊥AB于C，

∴BC=CA，PB=PA，

∴△PAO≌△PBO，

∴∠PBO=∠PAO=90°，

∴PB为⊙O的切线；

（2）解：连接AD，

∵BD为直径，∠BAD=90°由（1）知∠BCO=90°

∴AD∥OP，

∴△ADE∽△POE，

∴ = ，

由AD∥OC得AD=2OC

∵tan∠ABE= ，

∴ =

设OC=t，则BC=2t，AD=2t，由△PBC∽△BOC，

得PC=2BC=4t，OP=5t，

∴ = = ．

可设EA=2，EP=5，则PA=3，

∵PA=PB，

∴PB=3，

∴sin∠E= = ．

【解析】（1）要证PB是⊙O的切线，只要连接OA，再证∠PBO=90°即可；（2）连接AD，证明△ADE∽△POE，得到 = ，设OC=t，则BC=2t，AD=2t，由△PBC∽△BOC，可求出sin∠E的值．