【题目】墨墨和茗茗两人在做抛掷硬币的实验,他们同时各自抛一枚硬币,出现的结果及部分数据如表:
事件 | 两个正面 | 一正一反 | 两个反面 |
频数 |
| ________ |
|
频率 | ________ |
| ________ |
![]() 填写表中空格;
填写表中空格;
![]() 他们各自抛了多少次硬币?
他们各自抛了多少次硬币?
![]() 他们实验的结果可靠吗?说明理由.
他们实验的结果可靠吗?说明理由.
参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() 次;(3)可靠,理由详见解析.
次;(3)可靠,理由详见解析.
【解析】
(1)利用图表中数据得出出现两个正面向上和两个反面向上的频率,进而求出总数,分别得出答案即可;
(2)利用(1)中所求即可得出抛掷硬币的次数;
(3)利用模拟实验的可靠性分析得出即可.
(1)由图表可得出:出现两个正面向上和两个反面向上的频率为:10.53=0.47,
又∵出现两个正面向上和两个反面向上的频数为:48+46=94,
∴总数为:94÷0.47=200,
∴一正一反的频数为:20094=106,
48÷200=0.24,46÷200=0.23;
故答案为:106,0.24,0.23;
![]() 由
由![]() 得出他们各自抛了
得出他们各自抛了![]() 次硬币;
次硬币;
![]() 可靠,理由:因为试验次数较多,所以此次试验可靠.
可靠,理由:因为试验次数较多,所以此次试验可靠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小明设计两个可以自由转动的转盘,甲转盘被等分成
 个扇形,乙转盘被等分成
个扇形,乙转盘被等分成 个扇形,每个扇形上都标有相应的数字.小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于
个扇形,每个扇形上都标有相应的数字.小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于 ,小颖获胜;指针所指区域内的数字之和等于
,小颖获胜;指针所指区域内的数字之和等于 ,为平局;指针所指区域内的数字之和大于
,为平局;指针所指区域内的数字之和大于 ,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.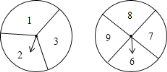
 转动转盘甲,转盘停止后,指针指向偶数的概率是________.
转动转盘甲,转盘停止后,指针指向偶数的概率是________. 在此游戏中,小颖获胜的概率是________.
在此游戏中,小颖获胜的概率是________. 你认为该游戏是否公平?若游戏规则公平,请说明理由;若游戏规则不公平,如果让你修改小明的方案,你认为应该从哪个方面入手(不用另外设计方案,只说明修改要点).
你认为该游戏是否公平?若游戏规则公平,请说明理由;若游戏规则不公平,如果让你修改小明的方案,你认为应该从哪个方面入手(不用另外设计方案,只说明修改要点). -
科目: 来源: 题型:
查看答案和解析>>【题目】建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.

(1)操作:
过点A作AD⊥
 于点D,过点B作BE⊥
于点D,过点B作BE⊥ 于点E.求证:△CAD≌△BCE.
于点E.求证:△CAD≌△BCE.(2)模型应用:
①如图2,在直角坐标系中,直线
 :
: 与y轴交于点A,与x轴交于点B,将直线
与y轴交于点A,与x轴交于点B,将直线 绕着点A顺时针旋转45°得到直线
绕着点A顺时针旋转45°得到直线 .求直线
.求直线 的函数表达式.
的函数表达式.②如图3,在直角坐标系中,点B(4,3),作BA⊥y轴于点A,作BC⊥x轴于点C,P是直线BC上的一个动点,点Q(a,5a﹣2)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图案中,是轴对称图形的是( )
A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, 、
、 分别平分
分别平分 ,
, ,则
,则 ________,若
________,若 、
、 分别平分
分别平分 ,
, 的外角平分线,则
的外角平分线,则 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某联欢会上有一个有奖游戏,规则如下:有
 张纸牌,背面都是喜羊羊头像,正面有
张纸牌,背面都是喜羊羊头像,正面有 张是笑脸,其余
张是笑脸,其余 张是哭脸.现将
张是哭脸.现将 张纸牌洗匀后背面朝上摆放到桌上,若翻到的纸牌中有笑脸就有奖,没有笑脸就没有奖.
张纸牌洗匀后背面朝上摆放到桌上,若翻到的纸牌中有笑脸就有奖,没有笑脸就没有奖. 小芳获得一次翻牌机会,她从中随机翻开一张纸牌.小芳得奖的概率是________.
小芳获得一次翻牌机会,她从中随机翻开一张纸牌.小芳得奖的概率是________. 小明获得两次翻牌机会,他同时翻开两张纸牌.小明认为这样得奖的概率是小芳的两倍,你赞同他的观点吗?请用树形图或列表法进行分析说明.
小明获得两次翻牌机会,他同时翻开两张纸牌.小明认为这样得奖的概率是小芳的两倍,你赞同他的观点吗?请用树形图或列表法进行分析说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
相关试题

