【题目】如图,![]() 中,
中,![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() ,
,![]() ,则
,则![]() ________,若
________,若![]() 、
、![]() 分别平分
分别平分![]() ,
,![]() 的外角平分线,则
的外角平分线,则![]() ________.
________.

参考答案:
【答案】![]()
![]()
【解析】
首先根据三角形内角和求出∠ABC+∠ACB的度数,再根据角平分线的性质得到∠IBC=![]() ∠ABC,∠ICB=
∠ABC,∠ICB=![]() ∠ACB,求出∠IBC+∠ICB的度数,再次根据三角形内角和求出∠I的度数即可;
∠ACB,求出∠IBC+∠ICB的度数,再次根据三角形内角和求出∠I的度数即可;
根据∠ABC+∠ACB的度数,算出∠DBC+∠ECB的度数,然后再利用角平分线的性质得到∠1=![]() ∠DBC,∠2=
∠DBC,∠2=![]() ECB,可得到∠1+∠2的度数,最后再利用三角形内角和定理计算出∠M的度数.
ECB,可得到∠1+∠2的度数,最后再利用三角形内角和定理计算出∠M的度数.
∵∠A=100°.
∵∠ABC+∠ACB=180°﹣100°=80°.
∵BI、CI分别平分∠ABC,∠ACB,∴∠IBC=![]() ∠ABC,∠ICB=
∠ABC,∠ICB=![]() ∠ACB,∴∠IBC+∠ICB=
∠ACB,∴∠IBC+∠ICB=![]() ∠ABC+
∠ABC+![]() ∠ACB=
∠ACB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×80°=40°,∴∠I=180°﹣(∠IBC+∠ICB)=180°﹣40°=140°;
×80°=40°,∴∠I=180°﹣(∠IBC+∠ICB)=180°﹣40°=140°;
∵∠ABC+∠ACB=80°,∴∠DBC+∠ECB=180°﹣∠ABC+180°﹣∠ACB=360°﹣(∠ABC+∠ACB)=360°﹣80°=280°.
∵BM、CM分别平分∠ABC,∠ACB的外角平分线,∴∠1=![]() ∠DBC,∠2=
∠DBC,∠2=![]() ECB,∴∠1+∠2=
ECB,∴∠1+∠2=![]() ×280°=140°,∴∠M=180°﹣∠1﹣∠2=40°.
×280°=140°,∴∠M=180°﹣∠1﹣∠2=40°.
故答案为:140°;40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】材料理解:如图1点P,Q是标准体育场400m跑道上两点,沿跑道从P到Q既可以逆时针,也可以顺时针,我们把沿跑道从点P到点Q的顺时针路程与逆时针路程的较小者叫P、Q两点的最佳环距离.(如图1,PQ顺时针的路程为120m,逆时针的路程为280m,则PQ的最佳环距离为120m).
问题提出:一次校运动800m预决赛中,如图2有甲、乙两名运动员他们同时同地从点M处出发,匀速跑步,他们之间的最佳环距离y(m)与乙用的时间x(s)之间的函数关系如图所示;解决以下问题:
(1)a=_________,乙的速度为___________.
(2)求线段BC的解析式,并写出自变量的范围.
(3)若本次运动会是1000m预决赛,甲完成比赛后是否有可能比乙多跑一圈,计算说明.


-
科目: 来源: 题型:
查看答案和解析>>【题目】下列叙述中:
 任意一个三角形的三条高至少有一条在此三角形内部;
任意一个三角形的三条高至少有一条在此三角形内部; 以a,b,c为边
以a,b,c为边 b,c都大于0,且
b,c都大于0,且 可以构成一个三角形;
可以构成一个三角形; 一个三角形内角之比为3:2:1,此三角形为直角三角形;
一个三角形内角之比为3:2:1,此三角形为直角三角形; 有两个角和一条边对应相等的两个三角形全等;正确的有
有两个角和一条边对应相等的两个三角形全等;正确的有
 个.
个.A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】“今天你光盘了吗?”这是国家倡导“厉行节约,反对浪费”以来的时尚流行语.某校团委随机抽取了部分学生,对他们进行了关于“光盘行动”所持态度的调查,并根据调查收集的数据绘制了如下两幅不完整的统计图:

根据上述信息,解答下列问题:
(1)抽取的学生人数为;
(2)将两幅统计图补充完整;
(3)请你估计该校1200名学生中对“光盘行动”持赞成态度的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示.AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角∠ABC为45°,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD 是改造后的斜坡(点D在直线BC上),坡角∠ADC为31°.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.01m)[参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.601,
 ≈1.414].
≈1.414]. 
-
科目: 来源: 题型:
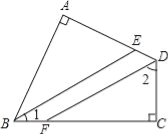
查看答案和解析>>【题目】四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.求证:
(1)、∠1+∠2=90°;(2)、BE∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中
 ,AO=BO,直线MN经过点O, 且AC⊥MN于C,BD⊥MN于D
,AO=BO,直线MN经过点O, 且AC⊥MN于C,BD⊥MN于D(1) 当直线MN绕点O旋转到图①的位置时,求证:CD=AC+BD;
(2) 当直线MN绕点O旋转到图②的位置时,求证:CD=AC-BD;
(3) 当直线MN绕点O旋转到图③的位置时,试问:CD、AC、BD有怎样的等量关系?请写出这个等量关系,并加以证明。

相关试题

