搜索
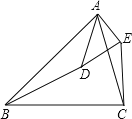
【题目】如图，在△ABC和△ADE中，∠BAD=∠CAE，∠ABC=∠ADE．
（1）求证：△ABC∽△ADE；
（2）判断△ABD与△ACE是否相似？并证明．
参考答案：
【答案】(1)见解析 (2) △ABD∽△ACE
【解析】
（1）由∠BAD=∠CAE易得∠BAC=∠DAE，这样结合∠ABC=∠ADE，即可得到△ABC∽△ADE．
（2）由（1）中结论易得
，从而可得： 
，这样结合∠BAD=∠CAE即可得到
△ABD∽△ACE了．
详解；
（1）∵∠BAD=∠CAE，
∴∠BAC=∠DAE，
∵∠ABC=∠ADE，
∴△ABC∽△ADE．
（2）△ABD∽△ACE，理由如下：
由（1）可知△ABC∽△ADE，
∴，
∴，
又∵∠BAD=∠CAE，
∴△ABD∽△ACE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在数轴上有三个点A、B、C，完成系列问题：
（1）将点B向右移动六个单位长度到点D，在数轴上表示出点D．
（2）在数轴上找到点E，使点E到A、C两点的距离相等．并在数轴上标出点E表示的数．
（3）在数轴上有一点F，满足点F到点A与点F到点C的距离和是9，则点F表示的数是 ．
-
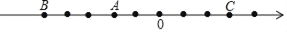
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知EF⊥AB，垂足为F，CD⊥AB，垂足为D，∠1=∠2，试判断∠AGD和∠ACB是否相等，为什么？（将解答过程补充完整） 解：∠AGD=∠ACB．理由如下：
∵EF⊥AB，CD⊥AB（已知）
∴∠EFB=∠CDB=90° （）
∴∥（同位角相等，两直线平行）
∴∠1=∠ECD（）
又∵∠1=∠2（已知）
∴∠ECD=（ 等量代换）
∴GD∥CB（）
∴∠AGD=∠ACB （）．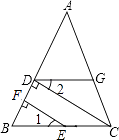
-
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，再求值：
（1）（x+2）（x﹣3）﹣x（x﹣4），其中x=﹣
（2）（a+b）（a﹣b）+（a+b）2﹣2a2 ， 其中a=3，b=﹣ ． -
科目： 来源： 题型：
查看答案和解析>>【题目】根据生物学研究结果，青春期男女生身高增长速度呈现如下图规律，由图可以判断，下列说法错误的是（ ）
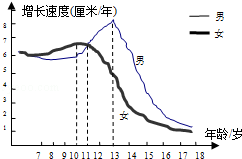
A.男生在13岁时身高增长速度最快
B.女生在10岁以后身高增长速度放慢
C.11岁时男女生身高增长速度基本相同
D.女生身高增长的速度总比男生慢 -
科目： 来源： 题型：
查看答案和解析>>【题目】在
中，
，
，垂足为
，
，
分别是
，
边上一点．
（1）求证：
；（2）若
，
，求
的度数． -
科目： 来源： 题型：
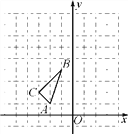
查看答案和解析>>【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(－2，1)，B(－1，4)，C(－3，2)．
(1)以原点O为位似中心，相似比为1∶2，在y轴的左侧，画出△ABC放大后的图形△A1B1C1，并直接写出C1点的坐标；
(2)若点D(a，b)在线段AB上，请直接写出经过(1)的变化后点D的对应点D1的坐标．
相关试题
