【题目】观察下列关于自然数的等式:
2×0+1=12①,
4×2+1=32②,
8×6+1=72③,
16×14+1=152④,
根据上述规律解决下列问题:
(1)完成第五个等式:32× +1= ;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
参考答案:
【答案】(1)30;312;(2)2n(2n﹣2)+1=(2n﹣1)2,验证见解析.
【解析】(1)根据2×0+1=12 ① 4×2+1=32② 8×6+1=72③ 16×14+1=152④可得第五个等式:32×30+1=312;(2)根据数字变化规律即可得出猜想,然后加以证明.
解:(1)30,312
(2)猜想: ![]()
证明:左边![]() 右边,
右边,
故![]()
“点睛”本题主要考查了数字变化规律,根据已知数字得出数字之间的变与不变是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有
 筐白菜,以每筐
筐白菜,以每筐 千克为标准重量,超过的千克数记为正数,不足的千克数记为负数换后的记录如下:
千克为标准重量,超过的千克数记为正数,不足的千克数记为负数换后的记录如下:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .回答下列问题上:
.回答下列问题上:(1)这
 筐白菜中最接近标准重量的这筐白菜重 千克.
筐白菜中最接近标准重量的这筐白菜重 千克.(2)与标准重量比较,
 筐白菜总计超过多少千克或不足多少千克?
筐白菜总计超过多少千克或不足多少千克?(3)若白菜每千克
 元,则出售这
元,则出售这 筐白菜可卖多少元?
筐白菜可卖多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】为使一个四边形木架不变形我们会从中钉一根木条,这是利用了三角形的____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=﹣x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.
(1)求△AOB的周长;
(2)设AQ=t>0,试用含t的代数式表示点P的坐标;
(3)当动点P,Q在直线l上运动到使得△AOQ与△BPO的周长相等时,记tan∠AOQ=m,若过点A的二次函数y=ax2+bx+c同时满足以下两个条件:
①6a+3b+2c=0;
②当m≤x≤m+2时,函数y的最大值等于
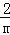 ,求二次项系数a的值.
,求二次项系数a的值.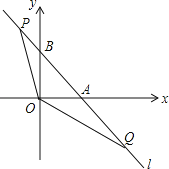
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,a、b、c、d、e、f均为有理数,图中各行、各列及两条对角线上三个数的和都相等,则a+b+c+d+e+f的值是_____.
4
﹣1
a
b
3
c
d
e
f
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(n,2)与B(-3,m)关于原点对称,则n-m等于( )
A. -1 B. -5 C. 1 D. 5
-
科目: 来源: 题型:
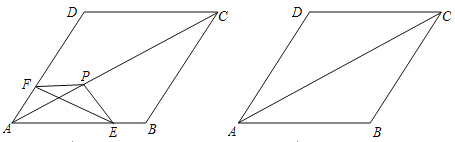
查看答案和解析>>【题目】
如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=
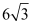 ,∠BAD=60°,且AB>
,∠BAD=60°,且AB>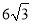 .
.⑴求∠EPF的大小;
⑵若AP=8,求AE+AF的值;
⑶若△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动,请直接写出AP长的最大值和最小值.
相关试题

