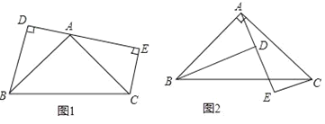
【题目】已知:如图1,AB=AC,点A是线段DE上一点,∠BAC=90°,BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,你能得到什么结论?并证明你的结论.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据全等三角形的判定证明△ADB≌△CEA即可求解;
(2)根据全等三角形的判定证明△ADB≌△CEA,即可得到结论.
证明:(1)∵BD⊥DE,CE⊥DE,
∴∠D=∠E=90°,
∴∠DBA+∠DAB=90°,
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠DBA=∠CAE,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∴DE=AD+AE=CE+BD;
(2)BD=DE+CE,理由是:
∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠ABD+∠EAC=90°,
∴∠BAD=∠EAC,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∵AE=AD+DE,
∴BD=CE+DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,求∠BCE的度数;
(2)如图2,当点D在线段BC上,如果∠BAC=60°,则∠BCE的度数;
(3)设∠BAC=α,∠BCE=β,如图3,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD.

(1)如图①,若∠ABE=30°,∠BEC=148°,求∠ECD的度数;
(2)如图②,若CF∥EB,CF平分∠ECD,试探究∠ECD与∠ABE之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为_______.

-
科目: 来源: 题型:
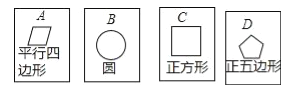
查看答案和解析>>【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,△ABC的三个顶点坐标分别为A(-4,1)、B(-1,1)、C(-4,3).
(1)画出Rt△ABC关于原点O成中心对称的图形Rt△A1B1C1;
(2)若Rt△ABC与Rt△A2BC2关于点B中心对称,则点A2的坐标为 、C2的坐标为 .
(3)求点A绕点B旋转180°到点A2时,点A在运动过程中经过的路程.

相关试题

