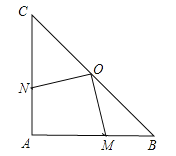
【题目】(本小题满分9分)如图,在![]() 中,∠A=90°,AB=AC=4 cm,若O是BC的中点,动点M在AB上移动,动点N在AC上移动,且AN=BM .
中,∠A=90°,AB=AC=4 cm,若O是BC的中点,动点M在AB上移动,动点N在AC上移动,且AN=BM .
(1)证明:OM = ON;
(2)在点M,N运动的过程中,四边形AMON的面积是否发生变化,若发生变化,请说明理由;若不变,请你求出四边形AMON的面积.
参考答案:
【答案】见解析
【解析】(1)连接OA(如图).
∵在Rt![]() ABC中,AB=AC,∴
ABC中,AB=AC,∴![]() ABC是等腰直角三角形,
ABC是等腰直角三角形,
∴∠ABC=45°,即∠ABO=45°.(2分)
∵O是BC的中点,且![]() ABC是等腰直角三角形,
ABC是等腰直角三角形,
∴AO⊥BC,
∴在![]() AOB中,∠OAB=90°∠ABO=90°45°=45°,
AOB中,∠OAB=90°∠ABO=90°45°=45°,
∴∠OAB=∠ABO,
∴OA=OB,
∵O是BC的中点,且![]() 是等腰直角三角形,∠BAC=90°,
是等腰直角三角形,∠BAC=90°,
∴![]() ,
,
∴∠OAC=∠ABO=45°,即∠OAN=∠OBM,(3分)
∵在![]() 与
与![]() 中
中
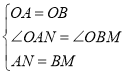 ,
,
∴![]() ,
,
∴ON=OM,即OM=ON.(5分)
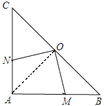
(2)在动点M、N运动的过程中,四边形AMON的面积不变.(6分)
理由如下:
连接OA.
由第(1)小题的证明可知:![]() ,
,
∴△OAN的面积等于![]() 的面积,
的面积,
∵四边形AMON的面积等于![]() 的面积与
的面积与![]() 的面积之和,
的面积之和,
∴四边形AMON的面积等于![]() 的面积与
的面积与![]() 的面积之和,
的面积之和,
∵![]() 的面积与
的面积与![]() 的面积之和等于
的面积之和等于![]() 的面积,
的面积,
∴四边形AMON的面积等于![]() 的面积,
的面积,
∵O是BC的中点,且![]() 是等腰直角三角形,
是等腰直角三角形,
∴△![]() 的面积的一半,(7分)
的面积的一半,(7分)
∵AB=AC=4 cm,
∴![]() 的面积为
的面积为![]() (cm2),
(cm2),
∴△OAB的面积为:![]() (cm2),
(cm2),
∴四边形AMON的面积为4 cm2.(9分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ma2﹣4ma+4m= .
-
科目: 来源: 题型:
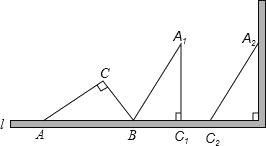
查看答案和解析>>【题目】如图,一个横截面为Rt△ABC的物体,∠ACB=90°,∠CAB=30°,BC=1m,工人师傅要把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1BC1的位置(BC1在l上),最后沿射线BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).
(1)请直接写出AB= ,AC= ;
(2)画出在搬动此物体的整个过程中A点所经过的路径,并求出该路径的长度.
(3)设O、H分别为边AB、AC的中点,在将△ABC绕点B顺时针方向翻转到△A1BC1的位置这一过程中,求线段OH所扫过部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,解答问题:
定义:线段AD把等腰三角形ABC分成△ABD与△ACD(如图1),如果△ABD与△ACD均为等腰三角形,那么线段AD叫做△ABC的完美分割线.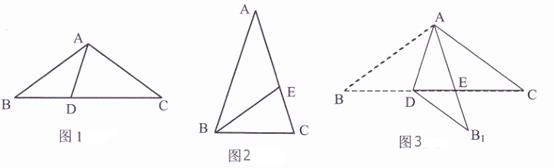
(1)如图1,已知△ABC中,AB=AC,∠BAC=108°,AD为△ABC的完美分割线,且BD<CD,则∠B= , ∠ADC=.
(2)如图2,已知△ABC中,AB=AC,∠A=36°,BE为△ABC的角平分线,求证:BE为△ABC完美分割线.
(3)如图3,已知△ABC是一等腰三角形纸片,AB=AC,AD是它的一条完美分割线,将△ABD沿直线AD折叠后,点B落在点B1处,AB1交CD于点E,求证:DB1=EC. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个圆柱体的侧面展开图为长方形ABCD,若AB=6.28cm,BC=18.84cm,则该圆柱体的体积是多少?(π取3.14,结果精确到十分位).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校积极响应上级的号召,举行了“决不让一个学生因贫困而失学”的捐资助学活动,其中6个班同学的捐款平均数如下表:
班级
一班
二班
三班
四班
五班
六班
捐款平均数(元)
6
4.6
4.1
3.8
4.8
5.2
则这组数据的中位数是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
A.y=﹣(x﹣1)2﹣3B.y=﹣(x+1)2﹣3
C.y=﹣(x﹣1)2+3D.y=﹣(x+1)2+3
相关试题

