【题目】已知抛物线y=a(x﹣m)2+n与y轴交于点A,它的顶点为点B,点A、B关于原点O的对称点分别为C、D.若A、B、C、D中任何三点都不在一直线上,则称四边形ABCD为抛物线的伴随四边形,直线AB为抛物线的伴随直线.
(1)如图1,求抛物线y=(x﹣2)2+1的伴随直线的解析式.
(2)如图2,若抛物线y=a(x﹣m)2+n(m>0)的伴随直线是y=x﹣3,伴随四边形的面积为12,求此抛物线的解析式.
(3)如图3,若抛物线y=a(x﹣m)2+n的伴随直线是y=﹣2x+b(b>0),且伴随四边形ABCD是矩形.
①用含b的代数式表示m、n的值;
②在抛物线的对称轴上是否存在点P,使得△PBD是一个等腰三角形?若存在,请直接写出点P的坐标(用含b的代数式表示);若不存在,请说明理由.
参考答案:
【答案】
(1)
解:由抛物线y=a(x﹣m)2+n与y轴交于点A,它的顶点为点B,
∴抛物线y=(x﹣2)2+1的与y轴交于点A(0,5),它的顶点为点B(2,1),
设所求直线解析式为y=kx+b,
∴ ![]() ,
,
解得: ![]() ,
,
∴所求直线解析式为y=﹣2x+5
(2)
解:如图,作BE⊥AC于点E,由题意得四边形ABCD是平行四边形,
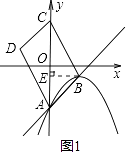
点A的坐标为(0,﹣3),
点C的坐标为(0,3),
可得:AC=6,
∵平行四边形ABCD的面积为12,
∴S△ABC=6即S△ABC= ![]() ACBE=6,
ACBE=6,
∴BE=2,
∵m>0,即顶点B在y轴的右侧,且在直线y=x﹣3上,
∴顶点B的坐标为(2,﹣1),
又抛物线经过点A(0,﹣3),
∴a=﹣ ![]() ,
,
∴y=﹣ ![]() (x﹣2)2﹣1
(x﹣2)2﹣1
(3)
解:①如图,作BF⊥x轴于点F,
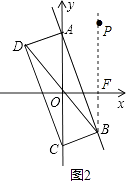
由已知可得A坐标为(0,b),C点坐标为(0,﹣b),
∵顶点B(m,n)在直线y=﹣2x+b(b>0)上,
∴n=﹣2m+b,即点B点的坐标为(m,﹣2m+b),
在矩形ABCD中,CO=BO.
∴b= ![]() ,
,
∴b2=m2+4m2﹣4mb+b2,
∴m= ![]() b,
b,
n=﹣2× ![]() b+b=﹣
b+b=﹣ ![]() b,
b,
②∵B点坐标为(m,n),即( ![]() b,﹣
b,﹣ ![]() b),
b),
∴BO= ![]() =b,
=b,
∴BD=2b,
当BD=BP,
∴PF=2b﹣ ![]() b=
b= ![]() b,
b,
∴P点的坐标为( ![]() b,
b, ![]() b);
b);
如图3,当DP=PB时,
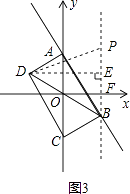
过点D作DE⊥PB,于点E,
∵B点坐标为( ![]() b,﹣
b,﹣ ![]() b),
b),
∴D点坐标为(﹣ ![]() b,
b, ![]() b),
b),
∴DE= ![]() b,BE=
b,BE= ![]() b,设PE=x,
b,设PE=x,
∴DP=PB= ![]() b+x,
b+x,
∴DE2+PE2=DP2,
∴ ![]() +x2=(
+x2=( ![]() b+x)2,
b+x)2,
解得:x= ![]() b,
b,
∴PF=PE+EF= ![]() b+
b+ ![]() b=
b= ![]() b,
b,
∴此时P点坐标为:( ![]() b,
b, ![]() b);
b);
同理P可以为( ![]() b,﹣
b,﹣ ![]() b);(
b);( ![]() b,
b, ![]() b),
b),
故P点坐标为:( ![]() b,
b, ![]() b);(
b);( ![]() b,
b, ![]() b);(
b);( ![]() b,﹣
b,﹣ ![]() b);(
b);( ![]() b,
b, ![]() b).
b).
【解析】(1)利用抛物线y=(x﹣2)2+1的与y轴交于点A(0,5),它的顶点为点B(2,1),求出直线解析式即可;(2)首先得出点A的坐标为(0,﹣3),以及点C的坐标为(0,3),进而求出BE=2,得出顶点B的坐标求出解析式即可;(3)①由已知可得A坐标为(0,b),C点坐标为(0,﹣b),以及n=﹣2m+b,即点B点的坐标为(m,﹣2m+b),利用勾股定理求出;②利用①中B点坐标,以及BD的长度即可得出P点的坐标.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
 .特别地,当点D、E重合时,规定:λA=0.另外,对λB、λC作类似的规定.
.特别地,当点D、E重合时,规定:λA=0.另外,对λB、λC作类似的规定.
(1)如图2,在△ABC中,∠C=90°,∠A=30°,求λA、λC;
(2)在每个小正方形边长均为1的4×4的方格纸上,画一个△ABC,使其顶点在格点(格点即每个小正方形的顶点)上,且λA=2,面积也为2;
(3)判断下列三个命题的真假(真命题打“√”,假命题打“×”):
①若△ABC中λA<1,则△ABC为锐角三角形;
②若△ABC中λA=1,则△ABC为直角三角形;
③若△ABC中λA>1,则△ABC为钝角三角形. . -
科目: 来源: 题型:
查看答案和解析>>【题目】建立模型:
如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
操作:
过点A作AD⊥l于点D,过点B作BE⊥l于点E.求证:△CAD≌△BCE.
模型应用:
(1)如图2,在直角坐标系中,直线l1:y=
 x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数按如图方式进行有规律的排列,第2行最后一个数是4,第3行最后一个数是7,第4行最后一个数是10,…,依此类推,第10行第2个数是__________,第__________行最后一个数是2 020.
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
5 6 7 8 9 10 11 12 13
…
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB交CD于O,OE⊥AB.
(1)若∠EOD=20°,求∠AOC的度数;
(2)若∠AOC:∠BOC=1:2,求∠EOD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点 O为数轴原点,点A表示的数是4,将线段OA沿数轴移动,移动后的线段记为O′A′.
(1)当点O′恰好是OA的中点时,数轴上点A′表示的数为 .
(2)设点A的移动距离AA′=x.
①当O′A=1时,求x的值;
②D为线段AA′的中点,点E在线段OO′上,且OE=
 OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.


-
科目: 来源: 题型:
查看答案和解析>>【题目】点O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处.射线OC平分∠MOB.
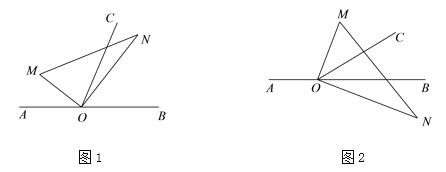
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=a,直接写出∠CON的度数(用含a的代数式表示);
(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,一边OM在射线OB上方,另一边ON在直线AB的下方.
①探究∠AOM和∠CON的度数之间的关系,写出你的结论,并说明理由;
②当∠AOC=3∠BON时,求∠AOM的度数.
相关试题

