【题目】点O为直线AB上一点，将一直角三角板OMN的直角顶点放在点O处．射线OC平分∠MOB．

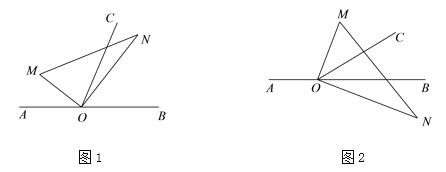
(1)如图1，若∠AOM=30°，求∠CON的度数；

(2)在图1中，若∠AOM=a，直接写出∠CON的度数（用含a的代数式表示）；

(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置，一边OM在射线OB上方，另一边ON在直线AB的下方．

①探究∠AOM和∠CON的度数之间的关系，写出你的结论，并说明理由；

②当∠AOC=3∠BON时，求∠AOM的度数．

参考答案：

【答案】(1) 15°;(2) ∠CON=a;(3) ①见解析；②144°.

【解析】

(1)根据角平分线的定义以及补角的定义,可求得∠CON的度数;

(2)可得∠CON=a;

(3) ①设∠AOM=a，可得，，可得∠AOM和∠CON的关系；

②由①知，，由∠AOC=3∠BON，可列方程，可得答案.

.

解：

(1)由已知得∠BOM=180°－∠AOM=150°，

又∠MON是直角，OC平分∠BOM，

所以∠CON=∠MON－∠BOM=90°－×150°=15°.

(2)∠CON=a.

(3)设∠AOM=a，则∠BOM=180°－a，

①∠AOM=2∠CON.

理由如下：

∵OC平分∠BOM，

∴

∵

∴

∴

②由①知

∴

解得

∴.

关闭