【题目】如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.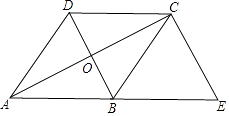
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AC=4 ![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.
参考答案:
【答案】
(1)证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形
(2)解:∵四边形BECD是平行四边形,
∴DB∥CE,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠E=∠OBA,
∴AC⊥CE.
在直角△ACE中,∵∠E=60°,AC=4 ![]() ,
,
∴CE= ![]() =
= ![]() =4.
=4.
∵四边形BECD是平行四边形,
∴BD=CE=4,
∴S菱形ABCD= ![]() ACBD=
ACBD= ![]() ×4
×4 ![]() ×4=8
×4=8 ![]() .
.
【解析】(1)由菱形的性质得AB=CD,AB∥CD,又用等量代换得出BE=CD,BE∥CD,根据平行四边形的判定定理得出结论;(2)由平行四边形的性质得DB∥CE,由菱形的性质得AC⊥BD,进而 根据平行线的性质得出∠E=∠OBA,AC⊥CE.解直角三角形得CE的长度,最后根据平行四边形的性质及菱形面积公式得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别延长□ABCD的边CD,AB到E,F,使DE=BF,连接EF,分别交AD,BC于G,H,连结CG,AH.
求证:CG∥AH.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B在线段AC的延长线上,AC<CB,点M、N分别是AC、BC的中点,点D是AB的中点.

(1)若AC=8cm,CB=10cm,求线段MN的长;
(2)若AC=a,CB=b,求线段CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了倡导节能低碳的生活,某公司对集体宿舍用电收费作如下规定:一间宿舍一个月用电量不超过a千瓦时,则一个月的电费为20元;若超过a千瓦时,则除了交20元外,超过部分每千瓦时要交
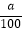 元.某宿舍3月份用电80千瓦时,交电费35元;4月份用电45千瓦时,交电费20元.
元.某宿舍3月份用电80千瓦时,交电费35元;4月份用电45千瓦时,交电费20元.
(1)求a的值;
(2)若该宿舍5月份交电费45元,那么该宿舍当月用电量为多少千瓦时? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,∠AEO=∠C,OE交BC于点F.
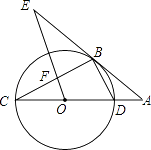
(1)求证:OE∥BD;
(2)当⊙O的半径为5,sin∠DBA= 时,求EF的长.
时,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收
费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部
分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数
据,回答:
月份
一
二
三
四
用水量(吨)
16
18
30
35
水费(元)
32
36
65
80
(1)a=________;b=________;
(2)若小明家五月份用水32吨,则应缴水费 元;
(3)若小明家六月份应缴水费102.5元,则六月份他们家的用水量是多少吨?
相关试题

