【题目】如图所示,一次函数y=kx+b的图象与反比例函数y=﹣![]() 的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是﹣2,
的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是﹣2,
(1)求一次函数的解析式;
(2)求△AOB的面积.
(3)直接写出kx+b+![]() >0的解集.
>0的解集.

参考答案:
【答案】(1)y=﹣x+2;(2)6;(3)由函数图象可得当x<﹣2或0<x<4时,kx+b+![]() >0.
>0.
【解析】试题分析:(1)先求出A,B两点坐标,将其代入一次函数关系式即可;
(2)根据一次函数与y轴的交点为(0,2),则△AOC和△BOC的底边长为2,两三角形的高分别为|x1|和|x2|,从而可求得其面积;
(3)由函数图象得出直线在双曲线上方时x的取值范围.
试题解析:(1)设A(x1,y1),B(x2,y2),则x1=﹣2,y2=﹣2,
把x1=y2=﹣2分别代入y=﹣![]() 得y1=x2=4,
得y1=x2=4,
∴A(﹣2,4),B(4,﹣2).
把A(﹣2,4)和B(4,﹣2)分别代入y=kx+b,
得![]() ,
,
解得![]() ,
,
∴一次函数的解析式为y=﹣x+2;
(2)如图,
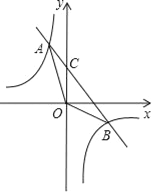
∵y=﹣x+2与y轴交点为C(0,2),
∴OC=2,
∴S△AOB=S△AOC+S△BOC=![]() ×OC×|x1|+
×OC×|x1|+![]() ×OC×|x2|=
×OC×|x2|=![]() ×2×2+
×2×2+![]() ×2×4=6;
×2×4=6;
(3)由函数图象可得当x<﹣2或0<x<4时,kx+b+![]() >0.
>0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当点P运动到CD上时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABD和△ACD关于直线AD对称;在射线AD上取点E,连接BE, CE,如图:在射线AD上取点F连接BF, CF,如图,依此规律,第n个图形中全等三角形的对数是( )

A.nB.2n-1C.
 D.3(n+1)
D.3(n+1) -
科目: 来源: 题型:
查看答案和解析>>【题目】将进货单价40元的商品按50元出售,能卖出500个,已知这种商品每涨价1元,就会少销售10个。为了赚得8000元的利润,售价应定为多少?这时应进货多少个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为a, P为正方形边上一动点,运动路线是A-D-C-B-A,设P点经 过的路程为x,以点A,P,D为顶点的三角形的面积是y,图象反映了y与x的关系,当
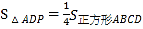 时,x=_____.
时,x=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线ll,l2交于点O,点P关于ll,l2的对称点分别为P1、P2.
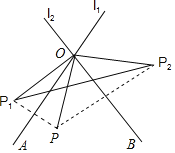
(1)若ll,l2相交所成的锐角∠AOB=60°,则∠P1OP2=______;
(2)若OP=3,P1P2=5,求△P1OP2的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,试判断AC与BC的位置关系,并说明理由.

相关试题

